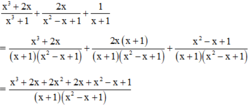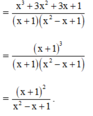1. Cộng hai phân thức cùng mẫu thức.
2. Cộng hai phân thức có mẫu thức khác nhau.
Phát biểu các qui tắc: Cộng hai phân thức cùng mẫu thức, cộng hai phân thức khác mẫu thức. Làm tính cộng:
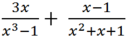
- Qui tắc cộng hai phân thức cùng mẫu:
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau và giữ nguyên mẫu thức.
- Qui tắc cộng hai phân thức khác mẫu:
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
- Làm tính cộng:
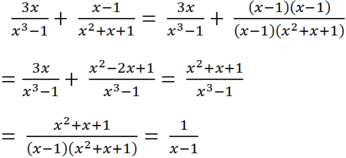
Phát biểu quy tắc : cộng hai phân thức cùng mẫu thức, cộng hai phân thức khác mẫu thức.
Làm tính cộng :
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
- Muốn cộng hai phân thức cùng mẫu, ta cộng các tử với nhau và giữ nguyên mẫu.
- Muốn cộng hai phân thức khác mẫu, ta quy đồng mẫu thức rồi cộng các phân thức cùng mẫu vừa tìm được.
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
\(=\dfrac{3x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{1}{x-1}\)
/ Cộng hai phân thức cùng mẫu:
2x / 5x - 2 + 4 / 5x - 2
ĐKXĐ: \(x\ne\dfrac{2}{5}\)
\(\dfrac{2x}{5x-2}+\dfrac{4}{5x-2}\) \(=\dfrac{2x+4}{5x-2}\)
Muốn qui đồng mẫu thức của nhiều phân thức có mẫu thức khác nhau làm thế nào ?
Hãy qui đồng mẫu thức của hai phân thức:
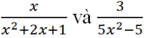
- Muốn qui đồng mẫu thức của nhiều phân thức ta có thể làm như sau:
+ Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung.
+ Tìm nhân tử phụ của mỗi mẫu thức.
+ Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
- Quy đồng mẫu hai phân thức trên:
Ta có: x2 + 2x + 1 = (x + 1)2 và 5x2 - 5 = 5(x2 – 1) = 5(x -1)(x + 1)
MTC: 5(x – 1)(x + 1)2
Nhân tử phụ tương ứng: 5(x – 1)(x + 1)
Ta có:
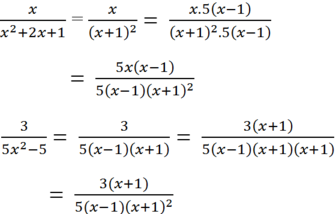
Cộng hai phân thức cùng mẫu (giúp mình vs, mìn đang cần gấp)
x + 1 / 2x - 2 + -2x / x2 - 1
ĐKXĐ: \(x\ne1;x\ne-1\)
\(\dfrac{x+1}{2x-2}+\dfrac{-2x}{x^2-1}\) \(=\dfrac{x+1}{2\left(x-1\right)}-\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\) \(=\dfrac{\left(x+1\right)^2}{2\left(x-1\right)\left(x+1\right)}-\dfrac{4x}{2\left(x-1\right)\left(x+1\right)}\) \(=\dfrac{x^2+2x+1-4x}{2\left(x-1\right)\left(x+1\right)}\) \(=\dfrac{x^2-2x+1}{2\left(x-1\right)\left(x+1\right)}\) \(=\dfrac{\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}\) \(=\dfrac{x-1}{2\left(x+1\right)}\)
Áp dụng qui tắc đổi dấu để các phân thức có cùng mẫu thức rồi làm tính cộng phân thức:
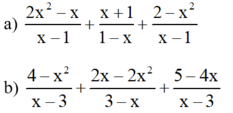
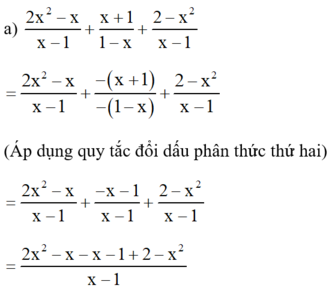
(Cộng các tử thức với nhau, giữ nguyên mẫu thức)
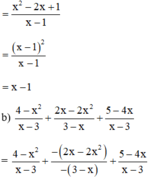
(Áp dụng quy tắc đổi dấu phân thức thứ hai)
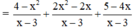
(Cộng các phân thức cùng mẫu thức)
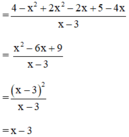
Cộng các phân thức khác mẫu thức: 5 3 x 2 y + 7 15 x y 2
Cộng các phân thức cùng mẫu thức: 1 - 2 x 6 x 3 y + 3 + 2 y 6 x 3 y + 2 x - 4 6 x 3 y
Cộng các phân thức khác mẫu thức: x 3 + 2 x x 3 + 1 + 2 x x 2 - x + 1 + 1 x + 1
Mẫu thức chung: x 3 + 1 = x + 1 x 2 - x + 1