0,abc = 1/a+b+c (a,b,c khác nhau và khác 0 )
Bạn nào đúng mình tik nhé
cho a/a+b =b/b+c =c/c+a
tính tổng a+b/2c +b+c/3a +c+a/4b ( với abc khác 0 và các mẫu đều khác 0)
các bạn giúp mình nhé
từ \(\frac{a}{a+b}=\frac{b}{b+c}=\frac{c}{c+a}\)
\(\Rightarrow\)\(\frac{a}{a+b}=\frac{b}{b+c}=\frac{c}{c+a}=\frac{a+b+c}{\left(a+b\right)+\left(b+c\right)+\left(c+a\right)}=\frac{a+b+c}{2.\left(a+b+c\right)}=\frac{1}{2}\)
vì a,b,c khác 0 và các mẫu đều khác 0 nên a = b = c
\(\Rightarrow\frac{a+b}{2c}+\frac{b+c}{3a}+\frac{c+a}{4b}=1+\frac{2}{3}+\frac{1}{2}=\frac{13}{6}\)
Tìm các chữ số a,b,c trong số thập phân 0,abc (a,b,c khác nhau và khác 0).Biết 0,abc=1:(a+b+c)
0,abc = 1: (a + b + c)
=> \(\frac{abc}{1000}=\frac{1}{a+b+c}\) => abc . (a+b +c) = 1000
Viết 1000 = 500.2 = 250.4 = 125.8 = 200 .5 = 100.10
thủ các cặp số trên, chỉ cố abc = 125 thỏa mãn
Vậy a = 1; b = 2; c = 5
cho a,b, c là số thực khác 0 và a+b+c khác 0 sao cho a+b+c/c =a-b+c/b=-a+b+c/a. Tính giá trị biểu thức M=(a+b)(b+c)(c+a)/abc
nếu đc giúp mk làm theo cách dãy tỉ số bằng nhau nhé giúp mk nhé mk cần gấp để nộp mong các bạn giúp mk .
Cảm ơn nhiều ạ <3
tìm các chữ số a, b ,c trong số thập phân 0. abc( a b c khác nhau và khác 0)
Biết 0. abc= 1: ( a+b+c)
Ta có: \(1\div\left(a+b+c\right)=\overline{0,abc}=\frac{\overline{abc}}{1000}\)
\(\Leftrightarrow\overline{abc}\times\left(a+b+c\right)=1000\)
Vì \(\overline{abc}\)là số có ba chữ số nên ta có các cách phân tích sau:
\(1000=500\times2=250\times4=200\times5=125\times8=100\times10\)
Thử từng trường hợp trong các trường hợp trên, chỉ có \(\overline{abc}=125\)là thỏa mãn.
Cho a; b; c> 0 đôi một khác nhau và khác 1, khẳng định nào sau đây là khẳng định đúng?
A. log a b 2 c b . log b c 2 a c . log c a 2 b a = 1
B. log a b 2 c b . log b c 2 a c . log c a 2 b a > 1
C. log a b 2 c b . log b c 2 a c . log c a 2 b a > - 1
D. log a b 2 c b . log b c 2 a c . log c a 2 b a < 1
Chọn A.
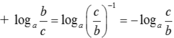
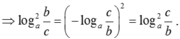
+ logab.logbc.logca = 1 khi logab.logba = logaa = 1 .
+ Từ 2 kết quả trên ta có 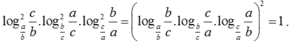
Thay các chữ a, b, c bằng các chữ số thích hợp trong mỗi phép tính sau ( mỗi chữ khác nhau được thay bởi mỗi chữ số khác nhau )
Ý a: ab,b - c,c = 0,a
Ý b: b,a - a,b = 2,7
Các bạn giải hộ mình nhé, mình đang cần gấp!!!!!!
a, \(\overline{ab,b}\) - \(\overline{c,c}\) = \(\overline{0,a}\)
(\(\overline{ab,b}\) - \(\overline{c,c}\)) \(\times\)10 = \(\overline{0,a}\)
\(\overline{abb}\) - \(cc\) = \(a\)
\(a\times\)100 + \(b\)\(\times\)11 - \(c\times\)11 = \(a\)
\(a\times\)100 + \(b\times\)11 - \(c\times\)11 - \(a\) = 0
\(a\times\)99 + \(b\) \(\times\)11 - \(c\times\) 11 = 0
11\(\times\)(\(a\times\)9 + \(b\) - \(c\)) = 0
\(a\times\) 9 + \(b\) - \(c\) = 0
\(a\times\) 9 = \(c-b\) ⇒ \(c-b\)⋮9 ⇒ \(c\) = \(b\) ; \(c\) - \(b\) = 9;
th: \(c\) = \(b\) ⇒ \(a\times\)9 = 0 ⇒ \(a\) = 0 (loại)
th: \(c-b=9\) ⇒ \(c=9+b\) ⇒ \(b\) = 0; \(c\) = 9
\(a\times\) 9 = 9 - 0 = 9 ⇒ \(a\) = 1
Vậy thay \(a=1;b=0;c=9\) vào biểu thức: \(\overline{ab,b}-\overline{c,c}=\overline{o,a}\) ta được:
10,0 -9,9 = 0,1
b, \(\overline{b,a}\) - \(\overline{a,b}\) = 2,7
(\(\overline{b,a}\) - \(\overline{a,b}\))\(\times\)10 = 2,7 \(\times\) 10
\(\overline{ba}\) - \(\overline{ab}\) = 27
\(b\times10+a-a\times10-b\) = 27
(\(b\times10\) - \(b\)) - (\(a\) \(\times\) 10 - \(a\)) = 27
(\(b\times10-b\times1\)) - (\(a\times\)10 - \(a\)\(\times\)1) = 27
\(b\)\(\times\)(10 -1) - \(a\) \(\times\)( 10 - 1) =27
\(b\times\) 9 - \(a\times9\) = 27
9\(\times\) (\(b-a\)) = 27
\(b-a\) = 27 : 9
\(b-a\) = 3 ⇒ \(b\) = 3 + \(a\) ≤ 9 ⇒ \(a\) ≤ 9 - 3 = 6
Lập bảng ta có:
| \(a\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(b\) = \(a+3\) | 3 | 4 | 5 | 6 | 7 | 8 |
9 |
Thay các giá trị của \(a;b\) lần lượt vào biểu thức \(\overline{b,a}-\overline{a,b}\) = 2,7 ta có:
3,0 - 0,3 = 2,7
4,1 - 1,4 = 2,7
5,2 - 2,5 = 2.7
6,3 - 3,6 = 2,7
8,5 - 5,8 = 2,7
9,6 - 6,9 = 2,7
Cho a,b,c đôi một khác nhau thỏa mãn điều kiện :
a/(b-c) +b/(c-a) + c/(a-b) = 0
Chứng minh rằng : a/(b-c)2 +b/(c-a)2 + c/(a-b)2 = 0
giúp mình vs mình cần gấp ,ai làm nhanh và đúng mình k nhé
\(\frac{a}{b-c}+\frac{b}{c-a}+\frac{c}{a-b}=0\)
=> \(\frac{a}{b-c}=-\frac{b}{c-a}-\frac{c}{a-b}=\frac{-b\left(a-b\right)-c\left(c-a\right)}{\left(c-a\right)\left(a-b\right)}=\frac{-ab+b^2-c^2+ac}{\left(a-b\right)\left(c-a\right)}\)
Nhân cả hai vế với \(\frac{1}{b-c}\)
=> \(\frac{a}{\left(b-c\right)^2}=\frac{-ab+b^2-c^2+ac}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
Tương tự: \(\frac{b}{\left(c-a\right)^2}=\frac{-bc+c^2-a^2+ba}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
\(\frac{c}{\left(a-b\right)^2}=\frac{-ca+a^2-b^2+cb}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
Cộng vế với vế ta có:
\(\frac{a}{\left(b-c\right)^2}+\frac{b}{\left(c-a\right)^2}+\frac{c}{\left(a-b\right)^2}\)
\(=\frac{-ab+b^2-c^2+ac-bc+c^2-a^2+ba-ca+a^2-b^2+cb}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=0\)
Vậy ta có điều phải chứng minh.
Thay a,b,c bằng các chữ số khác nhau và khác 0 thoả mãn :1/a+b+c=0,abc
https://friend20.com/vn/d20/quiz/69707687
Cho 3 Chữ Số a,b,c Khác Nhau Và Khác 0 . Tính Tổng Của Các Số Có 2 Chữ Số Khác Nhau Được Lập Từ 3 Chữ Số Đã Cho Biết a+b+c=8 ? Câu Hỏi Này Dành Cho Những Bạn Gái . Bạn Gái Nào Trả Lời Nhớ Kết Bạn Với Mình Nha .