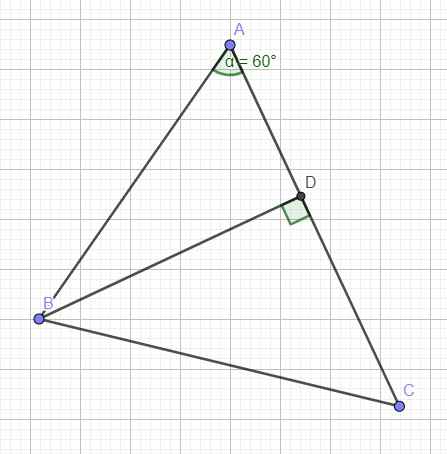
Cho ▲ABC có Â = 60 độ. Chứng tỏ rằng BC² = AB² + AC² - AB . AC

Những câu hỏi liên quan
Cho tam giác ABC có AB=8,AC=12 và Â=60 độ .Tính độ dài của cạnh BC ?
Kẻ đường cao BD ứng với AC
Trong tam giác vuông ABD:
\(\left\{{}\begin{matrix}cosA=\dfrac{AD}{AB}\\sinA=\dfrac{BD}{AB}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AD=AB.cosA=8.cos60^0=4\\BD=AB.sinA=8.sin60^0=4\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow CD=AC-AD=8\)
Trong tam giác vuông BCD, áp dụng định lý Pitago:
\(BC=\sqrt[]{BD^2+CD^2}=4\sqrt{7}\) (cm)
Đúng 1
Bình luận (0)
Cho ▲ABC có Â = 120º. Chứng minh rằng BC = AB² + AC² - AB.AC
Cho tam giác ABC có góc A = 60 độ. Chứng minh rằng BC^2 = AB^2 + AC^2 - AB x AC
Cho TG ABC có Â =60 độ. CMR:
BC^2= AB^2+AC^2-AB.AC
Tam giác ABC có Â=60 độ ; AB = 6 cm AC=8 cm .Tính BC
Xem thêm câu trả lời
cho tam giác ABC có Â = 120 độ. Trên tia phân giác của Â, lấy D sao cho AD=AB+AC. Chứng minh rằng tam giác BCD đều
cho tam giác ABC có Â = 120 độ. Trên tia phân giác của Â, lấy D sao cho AD=AB+AC. Chứng minh rằng tam giác BCD đều
Lấy sao cho mà nên
cân có nên là tam giác đều suy ra
Thấy (góc ngoài tại đỉnh của tam giác ) nên
Suy ra (hai góc tương ứng bằng nhau) và (hai cạnh tương ứng)
Lại có nên
cân tại có nên nó là tam giác đều.
Đây nhé!
Đúng 3
Bình luận (0)
Cho mình hỏi tại sao AC=AB+AC nên AE=AC? Tối nay mình pải nộp bài r
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A bằng 60 độ, chứng minh rằng BC2= AB2+AC2- AB*AC
Cho tam giác ABC (AB = AC, Â < 90ᴼ). Kẻ BH vuông góc với AC. Chứng minh rằng: AB^2 + AC^2 + BC^2 = 3. BH^2 + 2. AH^2 + CH^2
Xem chi tiết