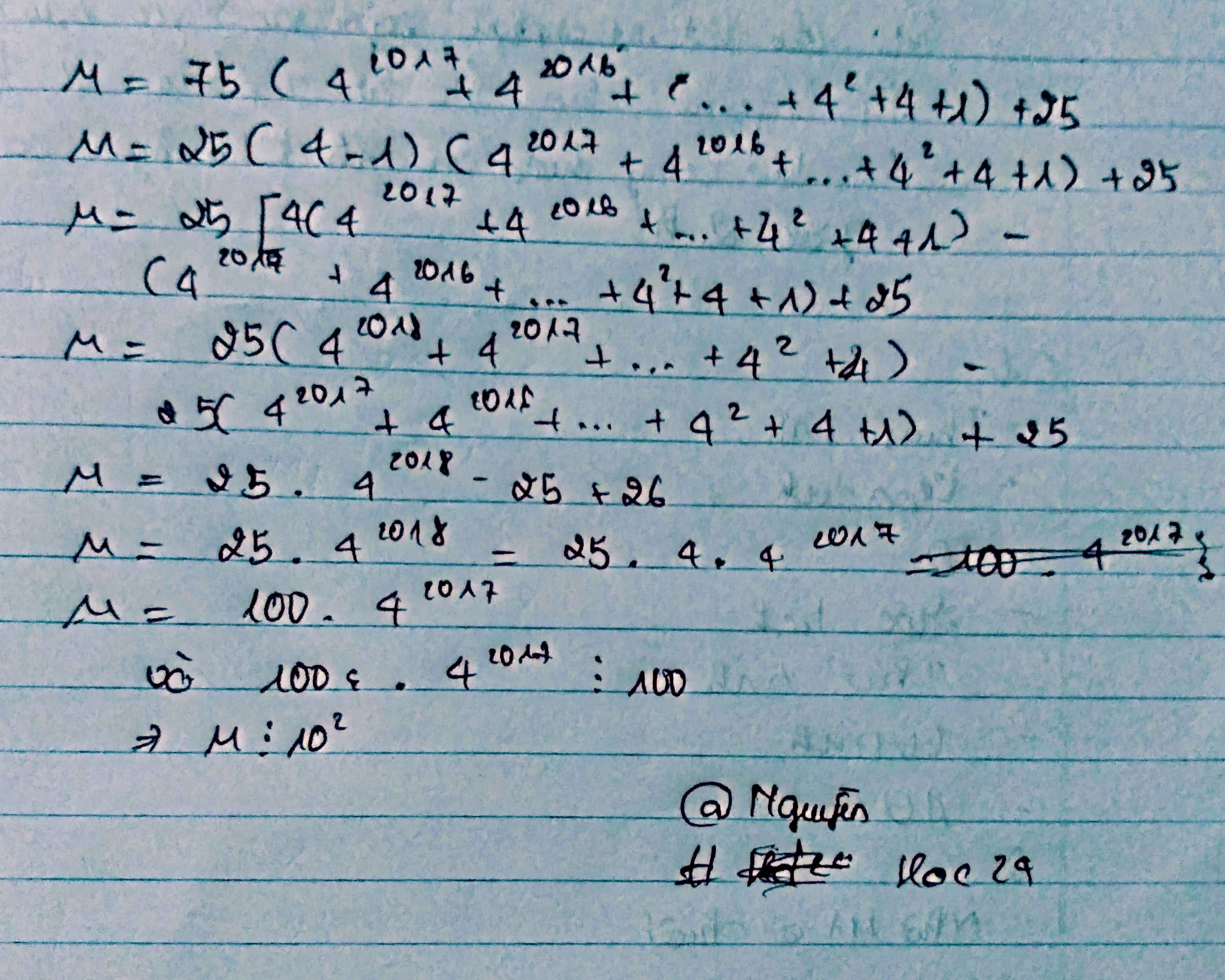\(CMR:\) \(M=\left[75\left(4^{2017}+4^{2016}+...+4^0\right)+25\right]⋮10\)

Những câu hỏi liên quan
a) CMR: \(A=\left(36^3+41^3\right)⋮7\)
b) CMR: \(A=\left[75\cdot\left(4^{2018}+4^{2017}+...+4^2+4+1\right)+25\right]⋮10\)
Chứng tỏ rằng \(M=75.\left(4^{2017}+4^{2016}+...+4^2+4+1\right)+25\) chia hết cho 102
A frac{frac{3}{4}-frac{3}{11}+frac{3}{13}}{frac{5}{4}-frac{5}{11}+frac{5}{13}}+frac{frac{1}{2}-frac{1}{3}+frac{1}{4}}{frac{5}{4}-frac{5}{6}+frac{5}{8}}B frac{2^{12}.3^5-4^6.9^2}{left(2^2.3right)^6+8^4.3^5}-frac{5^{10}.7^3-25^5.49}{left(125.7right)^3+5^9.14^3}C frac{left(a^{2016}+b^{2016}right)^{2017}}{left(c^{2016}+d^{2016}right)^{2017}} frac{left(a^{2017}-b^{2017}right)^{2016}}{left(c^{2017}-d^{2017}right)^{2016}}
Đọc tiếp
A = \(\frac{\frac{3}{4}-\frac{3}{11}+\frac{3}{13}}{\frac{5}{4}-\frac{5}{11}+\frac{5}{13}}+\frac{\frac{1}{2}-\frac{1}{3}+\frac{1}{4}}{\frac{5}{4}-\frac{5}{6}+\frac{5}{8}}\)
B = \(\frac{2^{12}.3^5-4^6.9^2}{\left(2^2.3\right)^6+8^4.3^5}-\frac{5^{10}.7^3-25^5.49}{\left(125.7\right)^3+5^9.14^3}\)
C = \(\frac{\left(a^{2016}+b^{2016}\right)^{2017}}{\left(c^{2016}+d^{2016}\right)^{2017}}\)= \(\frac{\left(a^{2017}-b^{2017}\right)^{2016}}{\left(c^{2017}-d^{2017}\right)^{2016}}\)
A = \(\frac{\frac{3}{4}-\frac{3}{11}+\frac{3}{13}}{\frac{5}{4}-\frac{5}{11}+\frac{5}{13}}+\frac{\frac{1}{2}-\frac{1}{3}+\frac{1}{4}}{\frac{5}{4}-\frac{5}{6}+\frac{5}{8}}\)
\(=\frac{3.\left(\frac{1}{4}-\frac{1}{11}+\frac{1}{13}\right)}{5.\left(\frac{1}{4}-\frac{1}{11}+\frac{1}{13}\right)}+\frac{\frac{1}{2}-\frac{1}{3}+\frac{1}{4}}{\frac{5}{2}.\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{4}\right)}\)
\(=\frac{3}{5}+\frac{1}{\frac{5}{2}}\)
\(=\frac{3}{5}+\frac{2}{5}=1\)
b) B = \(\frac{2^{12}.3^5-4^6.9^2}{\left(2^2.3\right)^6.8^4.3^5}-\frac{5^{10}.7^3:25^5.49}{\left(125.7\right)^3+5^9.14^3}\)
\(=\frac{2^{12}.3^5-\left(2^2\right)^6.\left(3^2\right)^2}{2^{12}.3^6+\left(2^3\right)^4.3^5}-\frac{5^{10}.7^3-\left(5^2\right)^5.7^2}{\left(5^3\right)^3.7^3+5^9.\left(7.2\right)^3}\)
\(=\frac{2^{12}.3^5-2^{12}.3^4}{2^{12}.3^6+2^{12}.3^5}-\frac{5^{10}.7^3-5^{10}-7^2}{5^9.7^3+5^9.7^3.2^3}\)
\(=\frac{2^{12}.3^4.\left(3-1\right)}{2^{12}.3^5\left(3+1\right)}-\frac{5^{10}.7^2.\left(7-1\right)}{5^9.7^3\left(1+2^3\right)}\)
\(=\frac{1}{3.2}-\frac{5.2}{7.3}\)
\(=\frac{7}{3.2.7}-\frac{5.2.2}{7.3.2}\)
\(=\frac{7}{42}-\frac{20}{42}\)
\(=-\frac{13}{42}\)
cs ng làm đung r
đag định lm
CMR :
\(75\left(4^{2018}+4^{2017}+...+42+4+1\right)+25⋮100\)
ta có 75(...) chia 100 dư 75
25 chia 100 dư 25
=> (75(....)+25)chia hết cho 100(tính chất chia hết của tổng)
học tốt
\(75\left(4^{2018}+4^{2017}+4^2+4+1\right)+25\)
\(=75\left(4^{2018}+4^{2017}+4^2+4\right)+75+25\)
\(=300\left(4^{2017}+4^{2016}+4+1\right)+100\)
Vì \(300\left(4^{2017}+4^{2016}+4+1\right)⋮100\)
và \(100⋮100\)nên
\(300\left(4^{2017}+4^{2016}+4+1\right)+100⋮100\)
Vậy \(75\left(4^{2018}+4^{2017}+4^2+4+1\right)+25⋮100\left(đpcm\right)\)
Tính tổng :
\(A=4^{2017}+4^{2016}+...+4^2+4+1\)
\(S=75.\left(1+4+4^2+...+4^{2016}+4^{2017}\right)+25\)
\(A=4^{2017}+4^{2016}+...+4^2+4+1\)
\(4A=4^{2018}+4^{2017}+...+4^3+4^2+4\)
\(4A-A=\left(4^{2018}+4^{2017}+...+4^3+4^2+4\right)-\left(4^{2017}+...+4+1\right)\)
\(3A=4^{2018}-1\)
\(A=\frac{4^{2018}-1}{3}\)
Đúng 0
Bình luận (0)
cm \(75\cdot\left(1+4+4^2+....+4^{2016}\right)+25\) chia hết cho\(4^{2017}\)
Chết bấm nhầm đấy, tôi chỉ có thể đóng góp dc thế này đây là bài tương tự hiểu thì áp dụng nhé
CMR D=75(42009+42008+...+4+1)+25 chia hết 400
D=75.16.42007+75.16.42006+...+75.4(=200)+75.1+25(=400)
D=400(3.42007+3.42006+...+1)chia hết cho 400
D chia hết cho 400
Đúng 0
Bình luận (0)
1) Cmr : \(A=75\left(4^{2015}+4^{2014}+4^{2013}+....+4^2+5\right)+25\)chia hết cho \(4^{2016}\)
đặt B = 42015 + 42014 + 42013 + ... + 42
4B = 42016 + 42015 + 42014 + ... + 43
4B - B = ( 42016 + 42015 + 42014 + ... + 43 ) - ( 42015 + 42014 + 42013 + ... + 42 )
3B = 42016 - 42
\(\Rightarrow\)B = \(\frac{4^{2016}-4^2}{3}\)hay B = \(\frac{4^{2016}-16}{3}\)
\(\Rightarrow\)A = 75 . ( \(\frac{4^{2016}-16}{3}\)+ 5 ) + 25
A = 75 . ( \(\frac{4^{2016}-16}{3}\)+ \(\frac{15}{3}\)) + 25
A = 75 . ( \(\frac{4^{2016}-1}{3}\)) + 25
A = 25 . ( 3 . \(\frac{4^{2016}-1}{3}\)) + 25
A = 25 . ( 42016 - 1 ) + 25
A = 25 . ( 42016 - 1 + 1 )
A = 25 . 42016 \(⋮\)42016
Đúng 0
Bình luận (0)
Cho A=\(\left(\dfrac{1}{2}-1\right).\left(\dfrac{1}{3}-1\right).\left(\dfrac{1}{4}-1\right)...\left(\dfrac{1}{2015}-1\right).\left(\dfrac{1}{2016}-1\right).\left(\dfrac{1}{2017}-1\right)\)
B=\(\left(-1\dfrac{1}{2}\right).\left(-1\dfrac{1}{3}\right).\left(-1\dfrac{1}{4}\right)...\left(-1\dfrac{1}{2015}\right).\left(-1\dfrac{1}{2016}\right).\left(-1\dfrac{1}{2017}\right)\)
Tính M=A.B
\(A=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{4}-1\right)...\left(\dfrac{1}{2015}-1\right)\left(\dfrac{1}{2016}-1\right)\left(\dfrac{1}{2017}-1\right)\\ A=\left(-\dfrac{1}{2}\right).\left(-\dfrac{2}{3}\right).\left(-\dfrac{3}{4}\right)...\left(-\dfrac{2014}{2015}\right)\left(-\dfrac{2015}{2016}\right)\left(-\dfrac{2016}{2017}\right)\\ A=\dfrac{1.2.3.4...2014.2015.2016}{2.3.4...2015.2016.2017}=\dfrac{1}{2017}\)
\(B=\left(-1\dfrac{1}{2}\right)\left(-1\dfrac{1}{3}\right)\left(-1\dfrac{1}{4}\right)...\left(-1\dfrac{1}{2015}\right)\left(-1\dfrac{1}{2016}\right)\left(-1\dfrac{1}{2017}\right)\\ B=\left(-\dfrac{3}{2}\right)\left(-\dfrac{4}{3}\right)\left(-\dfrac{5}{4}\right)...\left(-\dfrac{2016}{2015}\right)\left(-\dfrac{2017}{2016}\right)\left(-\dfrac{2018}{2017}\right)\\ B=\dfrac{3.4.5...2016.2017.2018}{2.3.4...2015.2016.2017}=\dfrac{2018}{2}=1009\)
\(M=A.B=\dfrac{1}{2017}.1009=\dfrac{1009}{2017}\)
Đúng 0
Bình luận (0)
Chứng minh rằng A=\(\left(4+4^2+4^3+...+4^{2016}\right)⋮21;420\)
A=\(\left(2016+2016^2+2016^3+...+2016^{2016}\right)⋮2017\)