Cho đường tròn tâm O bán kính AB.Gọi M là một điểm bất kì thuộc đườn tròn.CMR : Góc AMB = 90độ

Những câu hỏi liên quan
Cho đường tròn tâm O,đường kính AB.Gọi d và d' là các tiếp tuyến tại A và B của đường tròn tâm O.C là một điểm bất kì thuộc d,đường vuông góc với OC tại O cắt d' tại D .C/m CD là tiếp tuyến của đường tròn tâm O
Cho đưong tròn tâm O có bán kính R, đường kính AB. Qua điểm A kẻ đường thẳng d vuông góc AB tại A. Trên d lấy điểm C sao cho AC R. Lấy điểm M thuộc dưong tròn (O) sao cho OM vuông góc với CM tại M. a) Chứng minh 4 điểm A, C, O, M thuộc cùng một đường tròn. b) Gọi K là giao điểm thứ 2 của BC với đường tròn (O). Chứng minh: BC BK 4R mũ 2 c) Chứng minh: MB // OC d) Chứng minh: góc CMK gócMBCGIÚP MIK VỚI Ạ
Đọc tiếp
Cho đưong tròn tâm O có bán kính R, đường kính AB. Qua điểm A kẻ đường thẳng d vuông góc AB tại A. Trên d lấy điểm C sao cho AC >R. Lấy điểm M thuộc dưong tròn (O) sao cho OM vuông góc với CM tại M. a) Chứng minh 4 điểm A, C, O, M thuộc cùng một đường tròn. b) Gọi K là giao điểm thứ 2 của BC với đường tròn (O). Chứng minh: BC BK = 4R mũ 2 c) Chứng minh: MB // OC d) Chứng minh: góc CMK = gócMBC
GIÚP MIK VỚI Ạ
Cho nửa đường tròn tâm O bán kính CD. Từ C,D kẻ các tiếp tuyến Cx,Dy với nửa đường tròn tâm O.
Trên nửa đường tròn lấy điểm E, điểm M bất kì nằm trên CD(M khác C,D,O).Qua E kẻ đường thẳng vuông góc với EM và cắt Cx,Dy tại A,B.C/m góc AMB =90o
Vẽ đường tròn tâm O đường kính AB. M là một điểm bất kì thuộc Oa vẽ bán kính EF . Sao cho EF=OB. Vẽ tam giác MEF
Cho nữa đường tròn tâm O đường kính AB.Gọi Ax,By là các tia vuông góc với AB(Ax,By và nữa đường tròn cùng thuộc một nữa mặt phẳng bờ AB)Gọi M là 1 điểm bất kì thuộc tia Ax.Qua M kẽ tiếp tuyến với nữa đường tròn,cắt By ở N Chứng minh rằng
Tam giác MON vuông
MN=AM+BN
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Chứng minh rằng AM.BN
R
2
(R là bán kính của nửa đường tròn)
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Chứng minh rằng AM.BN = R 2 (R là bán kính của nửa đường tròn)
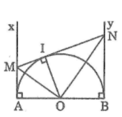
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2
Đúng 0
Bình luận (0)
cho đường tròn tâm O, đường kính AB có dây CD vuông góc với AB.Gọi M là điểm bất kỳ thuộc nửa đường tròn. (MC không song song với AB),E là giao điểm của MD và AB cmr EA/EB=FA/FB
Cho nửa đường tròn tâm O bán kính R đường kính AB.Gọi Ax,By là các tia vuông góc với AB (Ax,By và nửa đường tròn thuộc cùng 1 nửa mặt phẳng bờ AB).Qua điểm M nằm trên nửa đường tròn (M khác Avà B), vẽ đường thẳng vuông góc với MO,đường thẳng này cắt Ax,By theo thứ tự tại C và D . đường thẳng DO cắt tia đối của tia Ax tại I
Chứng minh CO vuông góc AM và tam giác CID cân
Đọc tiếp
Cho nửa đường tròn tâm O bán kính R đường kính AB.Gọi Ax,By là các tia vuông góc với AB (Ax,By và nửa đường tròn thuộc cùng 1 nửa mặt phẳng bờ AB).Qua điểm M nằm trên nửa đường tròn (M khác Avà B), vẽ đường thẳng vuông góc với MO,đường thẳng này cắt Ax,By theo thứ tự tại C và D . đường thẳng DO cắt tia đối của tia Ax tại I
Chứng minh CO vuông góc AM và tam giác CID cân
Cho đường tròn tâm O bán kính R và đường thẳng(Δ)không có điểm chung với đường tròn tâm( O), H là hình chiếu vuông góc của O trên (Δ) .từ điểm M bất kì trên (Δ) ( M không trùng H), vẽ 2 tiếp tuyến MA, MB với đường tròn (O) (A,B là hai tiếp điểm ).Gọi I, K theo thứ tự là giao điểm của AB với OM và OH1. Chứng minh AB 2 .AK với 5 điểmM ,A ,O, B, H cùng thuộc đường tròn2 .Chứng minh OI.OH OK.OM R^23.trên đoạn OA lấy điểm N sao cho AN 2ON. đường trung trực của BN cắt OM ở E .tính tỉ sốdfrac{OE}{O...
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng(Δ)không có điểm chung với đường tròn tâm( O), H là hình chiếu vuông góc của O trên (Δ) .từ điểm M bất kì trên (Δ) ( M không trùng H), vẽ 2 tiếp tuyến MA, MB với đường tròn (O) (A,B là hai tiếp điểm ).Gọi I, K theo thứ tự là giao điểm của AB với OM và OH
1. Chứng minh AB = 2 .AK với 5 điểmM ,A ,O, B, H cùng thuộc đường tròn
2 .Chứng minh OI.OH = OK.OM = \(R^2\)
3.trên đoạn OA lấy điểm N sao cho AN = 2ON. đường trung trực của BN cắt OM ở E .tính tỉ số\(\dfrac{OE}{OM}\)











