Từ đỉnh góc từ A của hình thoi ABCD kẻ AH vuông góc với BC, chia cạnh BC thành 2 đoạn thẳng. HB = 7cm; HC = 18 cm. Tính AH; AC; BD
P/s : Giúp tớ nha :33
Những câu hỏi liên quan
giúp mình câu này :
Từ đỉnh góc từ A của hình thoi ABCD kẻ AH vuông góc với BC, chia cạnh BC thành 2 đoạn thẳng. HB = 7cm; HC = 18 cm. Tính AH; AC; BD.
từ đỉnh góc A của hình thoi ABCD kẻ đường cao AH chia cạnh BC thành 2 đoạn thẳng HB = 7CM, HC= 18CM. tính độ dài AH, AC,BD?
Từ đỉnh góc tù A cuả hình thoi ABCD kẻ đường cao AH chia BC thành 2 đoạn thẳng HB = 7 cm, HD = 18 cm. Tính AH, AC, BD
Cho hình thoi ABCD trong đó đường vuông góc kẻ từ đỉnh góc tù A đến cạnh BC chia đôi cạnh đó. Tính các góc hình thoi
Các bạn giúp mình với,sắp phải nộp bài rồ, thanks trước !!!!!!!!!
Tính AB , AD của hình chữ nhật ABCD biết đường vuông góc AH kẻ từ A đến BD chia đoạn BD thành 2 đoạn thẳng HD=9cm , HB=16cm
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
A. 15cm
B. 12cm
C. 10cm
D. 8cm
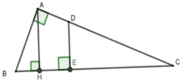
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).
Từ (1) và (2) suy ra
S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 3
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 (4)
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 18 = 5 6 => EC = 15cm.
Đáp án: A
Đúng 0
Bình luận (0)
1. Cho ∆ABC vuông tại A có AB=3 ,AC=4 kẻ đường cao AH . tính độ dài cạnh BC ,AH, HB ,HC 2. CHO ∆ABC vuông tại A đường cao AH . Biết AH=2,BH=1 . Tính độ dài các của ∆ABC 3. Cho hình chữ nhật ABCD , từ A kẻ đường thẳng vuông góc với BD và CD lần lượt tại H và E cho AB =4cm , AD=3cm a, Tính độ dài đường chéo BD của hình chữ nhật ABCD b; Tính AH
1.
\(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=1,8\left(cm\right)\\CH=\dfrac{AC^2}{BC}=3,2\left(cm\right)\\AH=\sqrt{3,2\cdot1,8}=5,76\left(cm\right)\end{matrix}\right.\)
Đúng 4
Bình luận (0)
2.
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC=HC\\AB^2=BH\cdot BC=BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}HC=4\left(cm\right)\\AB=\sqrt{HC+HB}=\sqrt{4+1}=\sqrt{5}\left(cm\right)\end{matrix}\right.\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-5}=2\sqrt{5}\left(cm\right)\)
Vậy \(AB=\sqrt{5}\left(cm\right);BC=5\left(cm\right);AC=2\sqrt{5}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho hình thoi ABCD trong đó đường vuông góc kẻ từ đỉnh góc tù A đến cạnh BC chia đôi cạnh đó. Tính các góc hình thoi
\(Help\)\(me\)\(!!!\)
Cho hình thoi ABCD có A > 90 độ. Trên BC lấy điểm H sao cho AH vuông góc với BC, HB= 7cm, HC= 8cm. Tính AH, AC, BD