Phần tự luận
Nội dung câu hỏi 1
Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH
a) Tính BC, AH, ∠B ; ∠C
Phần tự luận
Nội dung câu hỏi 1:
Cho tam giác ABC có AB = 6cm; AC = 8 cm; BC = 10 cm
a) Chứng minh tam giác ABC vuông
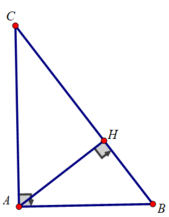
a) Xét tam giác ABC có:
A B 2 + A C 2 = 6 2 + 8 2 = 100 = B C 2
Tam giác ABC vuông tại A.
Phần tự luận
Nội dung câu hỏi 1
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
a) Tính BC, ∠B, ∠C
a) Xét tam giác ABC vuông tại A có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
⇒ BC = 10 (cm)

∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0
1Cho tam giác ABC cân tại A. Kẻ BH vuông với AC biết AH= 6cm HC= 3cm. Tính BC
2 Cho tam giác ABC vuông tại A có góc B=60độ CMR AB=1/2BC
Lê Xuân Trường
1-Xét tam giác ABH và tam giác ACH có
Góc AHB = Góc AHC = 90 độ
AC = AB (Do tam giác ABC cân tại A)
Góc ABH = Góc ACH(Do tam giác ABC cân tại A)
Suy ra tam giác ABH = tam giác ACH (cạnh huyền -góc nhọn )
Suy ra BH = CH =3 cm (2 cạnh tương ứng )
2 . Tui không biết làm thông cảm nhe !
Phần trắc nghiệm
Nội dung câu hỏi 1
Tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, BC = 25cm, khi đó AB bằng:
A. 20cm
B. 15cm
C. 34cm
D. 25/9
Câu hỏi 1:Tam giác ABC vuông tại A có BC = 30cm và AB:AC = 3:4. Khi đó AB = cm
Câu hỏi 2:Trong mặt phẳng tọa độ Oxy, vẽ điểm A(-3 ; 4). Khoảng cách từ A đến gốc tọa độ bằng
Câu hỏi :3Cho tam giác ABC vuông tại A; đường cao AH.
Biết BH = 9cm ; CH = 16cm. Tính độ dài AH.
Trả lời: AH = cm
1cho tam giác vuông cân tại a , trên cạnh ab lấy điểm d ( khác a và b ) , trên tia đói tia ac lấy điểm e sao cho ae =ad
a. cm cd=be ( em làm đc câu này rồi ạ)
b. cd vuông góc be
c, tia ed cắt cạnh bc tại m , so sánh mb và md
2 . cho tam giác abc có a =120 đọ . ab = 4cm, ac=6cm .gọi m là trung điểm bc . tinh am
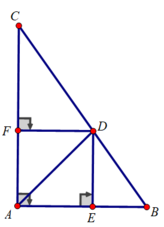
a) Chứng minh được: \(\Delta\)ABE = \(\Delta\)ACD => CD = BE
b ) \(\Delta\)ABE = \(\Delta\)ACD => ^ABE = ^ACD
Gọi H là giao điểm của CD và BE
=> ^HBD = ^ACD
Lại có: ^HDB = ^ADC ( đối đỉnh )
=> ^HBD + ^HDB = ^ACD + ^ADC = 90 độ
=> ^DHB = 180o - ( ^HBD + ^HDB ) = 90 độ
=> CD vuông BE
c) Xét \(\Delta\)EAD có: ^EAD = 90 độ và EA = ED => \(\Delta\)EAD vuông cân => ^EDA = 45 độ
=> ^MDB = ^EDA = 45 độ ( đối đỉnh )
Ta có: BD vuông AC ; CD vuông BE => D là trực tập \(\Delta\)ECB => ED vuông BC => ^DMB = 90 độ
Xét \(\Delta\)DMB có: ^DBM = 180o - ( ^MDB + ^DMB ) = 180 độ - ( 90o + 45o ) = 45o
=> ^MDB = ^DBM => \(\Delta\)DMB cân tại M => MB = MD
Bài 2: Theo cách lớp 7.
Kẻ BH vuông AC tại H => ^BAH = 180o - ^BAC = 180o - 120o = 60o
=> \(\Delta\)HBA là nửa tam giác đều ( học cái này chưa? )
=> AH = \(\frac{1}{2}\).AB = \(\frac{1}{2}\).4 = 2 ( cm )
Xét \(\Delta\)HAB vuông tại H có: AH = 2 cm ; AB = 4 cm
Dùng định lí Pitago => \(BH^2=AB^2-AH^2=4^2-2^2=12\)=> \(BH=2\sqrt{3}\)(cm)
Xét \(\Delta\)BHC vuông tại H có: \(BH=2\sqrt{3}\)cm ; HC = HA + AC = 2 + 6 = 8 cm
Theo định lí Pitago => \(BC^2=BH^2+HC^2=\left(2\sqrt{3}\right)^2+8^2=76\)=> \(BC=2\sqrt{19}\)( cm )
Vì M là trung điểm BC => \(BM=\sqrt{19}\)cm
Kẻ AK vuông BC tại K
Ta có: \(S\left(ABC\right)=\frac{1}{2}.BH.AC=\frac{1}{2}AK.BC\)( diện tích tam giác ABC )
=> \(BH.AC=AK.BC\)=> \(2\sqrt{3}.6=AK.2\sqrt{19}\Rightarrow AK=\frac{6\sqrt{57}}{19}\)cm
Xét \(\Delta\)BAK vuông tại K có: \(AB=4cm;AK=\frac{6\sqrt{57}}{19}\)cm
Theo định lí Pitago => \(BK^2=AB^2-AK^2\)=> \(BK=\frac{14\sqrt{19}}{19}\)cm
=>KM = BM - BK = \(\sqrt{19}-\frac{14\sqrt{19}}{19}=\frac{5\sqrt{19}}{19}\)cm
Xét \(\Delta\)AKM có: \(KM=\frac{5\sqrt{19}}{19}\)cm và \(AK=\frac{6\sqrt{57}}{19}\)cm
=> \(AM^2=AK^2+KM^2=\left(\frac{5\sqrt{19}}{19}\right)^2+\left(\frac{6\sqrt{57}}{19}\right)^2=7\)
=> \(AM=\sqrt{7}\)
Tam giác ABC vuông tại A, có đường cao AH , AB =3 cm, AC =4 cm. Hỏi AH = ?
Áp dụng Pytago trong tam giác vuông ABC ta đc:
\(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{3^2+4^2}=5cm\)
Áp dụng hệ thức lượng ta đc:
AB . AC = AH . BC
=> 3 . 4 = AH . 5
=> 12 = AH . 5
=> AH = 12/5 cm
Bài 1Cho tam giác ABC, 2 đường phân giác BD, CE cắt nhau tại I. Biết góc BIC=135 độ
a) CM tam giác ABC vuông
b)Gọi khoảng cách đến các cạnh tam giác ABC là r .CM r = (AB + AC -BC) :2
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. Gọi I,K,S là giao của các dg p/g của tam giác ABC,ABH,ACH
a) áp dụng kết quả bài trên CM AH=r + r1+r2. Trong đó r,r1,r2 lần lượt là khoảng cách từ giao điểm của các p?g trong tam giác ABC,ABH,ACH
b) Cm AI vuông góc với KS
Cho tam giác ABC vuông góc tại A có tổng độ dài hai cạnh AB và AC là 17,7 Cm biết rằng nếu giảm độ dài AB đi 4,9cm và giữ nguyên độ dài cạnh AC thì đọ dài AB gấp 3lần độ daì AC tính diện tích tam giác ABC
Câu hỏi tương tự Đọc thêm