cho tam giác ABC vuông cân tại A. Lấy D thuộc AB và E thuộc AC sao cho AD=AE. Qua D;A kẻ các đường vuông góc với BE cắt BC lần lượt tại I và K. M là giao điểm ID và CA
a)AM=AC
b)IK=KC
Những câu hỏi liên quan
tam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK KC
Đọc tiếp
tam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD = AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK = KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD = AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK = KCtam giác ABC vuông cân tại A , D thuộc AB , E thuộc AC sao cho AD = AE . Qua D và A kẻ các đường thẳng vuông góc với BE cắt BC lần lượt tại I và K . CM IK = KC
Cho tam giác ABC vuông tại A có AB = AC . Lấy điểm D thuộc cạnh AB , điểm E thuộc cạnh AC sao cho AD = AE . Đường thẳng đi qua D và vuông góc với BE cắt CA tại K. Chứng minh tam giác KDC là tam giác cân.
Cho tam giác giác ABC vuông tại A có AB = AC. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA tại K. Chứng minh rằng AK = AC.
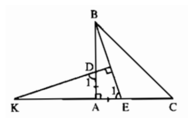
Từ (1) và (2) suy ra AK = AC (điều phải chứng minh ).
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông cân tại A, D thuộc AB, E thuộc AC sao cho AD=AE. Qua D vẽ đoạn thẳng vuông góc BE cắt BC tại K. Qua A vẽ đoạn thẳng vuông góc BE cắt BC tại H. Gọi M là giao điểm của DK và AC. CMR:
a) tam giác BAE = tam giác CAD (cái này mình biết làm rồi)
b) tam giác MDC cân
c) HK = HC
Cho tam giác ABC vuông tại A có AB=AC. Lấy D thuộc AB, E thuộc AC sao cho AD=AE. Đường thẳng đi qua D vuông góc với BE cắt AC ở K. CMR: AK=AC
Cho tam giác ABC vuông tại A có AB = AC. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng đi qua D và vuông góc với BE cắt đường thẳng CA ở K. Chứng minh AK = AC ?
Xét hai tam giác KAD và BAE có:
\(\widehat{KAD}=\widehat{BAE}\left(=90^o\right)\)
AD = AE (gt)
\(\widehat{D_1}=\widehat{E_1}\) (cùng phụ với góc K)
Vậy: \(\Delta KAD=\Delta BAE\left(g-c-g\right)\)
Suy ra: AK = AB (hai cạnh tương ứng)
Ta lại có AB = AC
Do đó: AK = AC.
Đúng 0
Bình luận (0)
Xet tứ giác ADIE ta có: góc D3+ E =180
> D3=180- E.
> D4=180-D1
[ Góc D3 =D4 (đối đỉnh)]
>> góc D1= E.
xét tam giác ABE và tam giác KAD. Có góc D1=E, cạnh AD=AE,
---> Tam giác ABE = tam giác KAD.
-->> AB =AK
> AB=AC=KA
AK=AC.
>>
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Lấy điểm E thuộc cạnh AB , lấy điểm D thuộc tia đối của tia CA sao cho: AE + AD = AB + AC. Kẻ đường thẳng qua C và song song với DE cắt đường thẳng qua E và song song với DC tại F. Chứng minh rằng: a)C/m tam giác EFC = tam giác CDE . b) C/m tam giác FEB cân
Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE
So sánh góc ABD và ACE
Xét ΔABD và ΔACE có:
AB = AC (gt)
Góc A chung
AD = AE (gt)
Nên ΔABD = ΔACE ( c.g.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và AB = AC = 5cm. Cho D thuộc AB, E thuộc AC sao cho AD = AE. Đường thẳng a đi qua D vuông góc với BE và cắt CA tại K. Tính CK.