BC(120;180;90) = B( )

Những câu hỏi liên quan
cho tam giác ABC có B=120,BC=c,AC=b.tinh BC theo b,c
minhf vt goiwj ys hoy
bạn dùng công thức trong tam giác thường:
b2 = a2 + c2 - 2.ac.cosB (tức là AC2 = BC2 + AB2 - 2.AB,BC.cosB)
tính đc AC = x
trên tia BC, vẽ BE=BA sao cho E&C nằm khác phía so với B. dễ dang chứng minh dc tam giác ABE là tam giác đều. Hạ AH vuông góc với BE
=> AH=AB.sin60
tính dc AH=y
Trong tam giác AHC có AC=x, AH=y
=> sinC=AH/AC
=>trị số góc C
=>góc BDC = 180 - (gócC + 60) (trong tam giác BCD ý) =>sin(BDC)
dùng định lý hàm số sin
=> BD = BC*(sinC/sinBDC)
Đúng 0
Bình luận (0)
Áp dụng định lý hàm số COS ta có:
AC^2 = AB^2+AC^2 - 2AB.AC.cosB
= 12^2 + 6^2 -2.12.6.(-1/2) = 252 ------> AC = CĂN 252
Vì BD là phân giác của góc B nên theo tính chất ta có:
AD/AC =AB/BC = 6/12 = 1/2
----> DC = 2 AD , mà AC = CĂN 252 ------> AD= 1/3 căn 252
Áp dụng định lý hàm số COS đồi với tam giác ABD có:
AD^2=AB^2+BD^2 - 2AB.BD.cosB
<=>(1/3 căn 252)^2= 6^2+ BD^2 - 2.6.BD.(1/2)
<=> BD^2 - 6BD + 8 =0
<=> BD = 4 hoặc BD =2
Vậy: BD = 4 (cm)
Trên đây là bài giải với ĐK: BD là phân giác trong.
còn nếu BD là phân giác ngoài thì tỉ lệ: AC/AD =AB/BC
DO VẬY BD = 8 cm
Đúng 0
Bình luận (0)
tìm x biết
a) x∈BC(2,5;15) và x < 120
b) x∈BC(8;15;40) và 250 < x ≤ 400
\(a,BC\left(2,5,15\right)=B\left(30\right)=\left\{0;30;60;90;120;...\right\}\\ \Rightarrow x\in\left\{0;30;60;90\right\}\\ b,BC\left(8,15,40\right)=B\left(120\right)=\left\{0;240;360;480;...\right\}\\ \Rightarrow x=360\)
Đúng 3
Bình luận (2)
cho tam giác ABC, góc A=120 độ, AB=c, BC=a, AC=b. C/m: a2=b2+c2+bc
1.Hãy tìm các tập B(8),B(120) và BC(8,12)
2.Hãy tìm BCNN(105,140) rồi tìm BC(105,140)
1. B(8)=(8,16,24,32,40,48...) B(120)=(120,240,480,960...) BC(8,12)= (0,24,48...)
2.BCNN(105,140)=420 và BC(105,140)=B(420)=(0,420,840...)
Đúng 0
Bình luận (0)
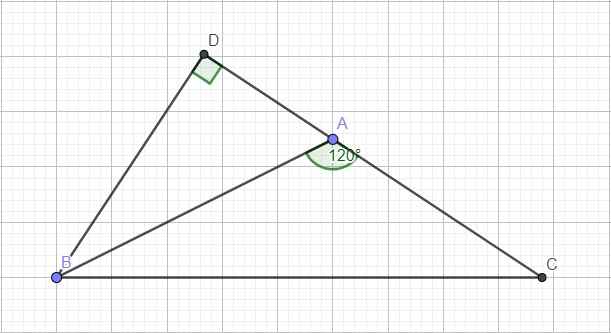
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
Tam giác ABC có Â=120 độ . BC = a; AC=b; AB =c Cm rằng: a^2=b^2+c^2+bc
Cho tam giác ABC có A=120 độ, BC=a;AC=b;AB=c . CMR a^2=b^2+c^2+bc
Số nào sau đây thuộc tập hợp BC (15.20)? 120 100 30 40
Giải tam giác ABC có góc B = 120\(^o\),AB=70m,BC = 18m
Cho tam giác ABC. Trên BC lấy điểm M sao cho BM = 1 3 BC. Biết diện tích tam giác ABC bằng 120 cm2. Tính S.ABM.
Lời giải:
$\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{1}{3}$
$\Rightarrow S_{ABM}=\frac{1}{3}\times S_{ABC}=\frac{1}{3}\times 120=40$ (cm2)
Đúng 1
Bình luận (0)