Hãy xác định hàm số bậc nhất thỏa mãn mỗi điều kiện sau
Đồ thị hàm số đi qua 2 điểm M\(\left(-2;9\right)\)và cắt đường thẳng (d): 3x-5y=1 tại điểm có hoành độ bằng 2
Những câu hỏi liên quan
Hãy xác định hàm số bậc nhất thỏa mãn mỗi điều kiện sau: Đồ thị hàm số đi qua hai điểm M(-3; 1) và N(1; 2)
Hàm số bậc nhất có dạng y = ax + b (a ≠ 0)
Đồ thị hàm số y = ax + b đi qua M(-3; 1) và N(1; 2) nên tọa độ của M và N nghiệm đúng phương trình hàm số.
Điểm M: 1 = -3a + b
Điểm N: 2 = a + b
Hai số a và b là nghiệm của hệ phương trình:
Đúng 0
Bình luận (0)
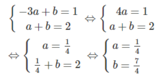
Hãy xác định hàm số bậc nhất thỏa mãn mỗi điều kiện sau: Đồ thị hàm số đi qua hai điểm M( 2 ; 1) và N(3; 3 2 - 1)
Hàm số bậc nhất có dạng y = ax + b (a ≠ 0)
Đồ thị hàm số y = ax + b đi qua M( 2 ; 1) và N(3; 3 2 - 1) nên tọa độ của M và N nghiệm đúng phương trình hàm số.
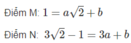
Hai số a và b là nghiệm của hệ phương trình:
Đúng 0
Bình luận (0)
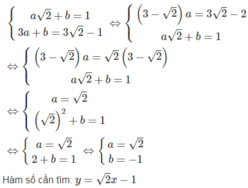
Hãy xác định hàm số bậc nhất thỏa mãn mỗi điều kiện sau:
a/ Đồ thị của hàm số đi qua 2 điểm M(-3:1) và N(1:2)
a.
ax+b=y
M(-3,1) → x=-3; y=1
N(1;2) → x=1 ' y=2
Hãy xác định hàm số bậc nhất thỏa mãn mỗi điều kiện sau: Đồ thị đi qua điểm M(-2; 9) và cắt đường thẳng (d): 3x – 5y = 1 tại điểm có hoành độ bằng 2.
Hàm số bậc nhất có dạng y = ax + b (a ≠ 0)
Điểm N nằm trên đường thẳng (d): 3x – 5y = 1 có hoành độ bằng 2 nên tung độ của N bằng: 3.2 - 5y = 1 ⇔ -5y = -5 ⇔ y = 1
Điểm N( 2; 1)
Đồ thị hàm số y = ax + b đi qua M(-2; 9) và N(2; 1) nên tọa độ của M và N nghiệm đúng phương trình hàm số.
Điểm M: 9 = -2a + b
Điểm N: 1 =2a + b
Hai số a và b là nghiệm của hệ phương trình:
Đúng 0
Bình luận (0)
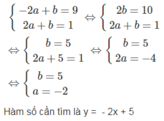
Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:
a = 3 và đồ thị của hàm số đi qua điểm A(2; 2)
Với a = 3 hàm số có dạng y = 3x + b.
Đồ thị hàm số đi qua điểm (2; 2), nên ta có:
2 = 3.2 + b => b = 2 – 6 = - 4
Vậy hàm số là y = 3x – 4
Đúng 0
Bình luận (0)
cho hàm số bậc nhất y=ax-3(1) hãy xác định hệ số a trong mỗi trường hợp sau
a, đồ thị hàm số (1) di qua điểm M(1/2;-2)
b,đồ thị hàm số (1) cắt đường thẳng y=-3x+2 tại điểm có tung độ bằng 5
a, ĐỒ thị hàm số (1) đi qua điểm M(1/2;-2 )
<=> -2 = 1/2.a -3
<=> 1/2.a= -2+3
<=> 1/2.a = 1
<=> a = 2
b, Ta có tọa độ giao điểm của đồ thị hàm số ( 1) và độ thị hàm số y= - 3x + 2 ( đặt là 1' )là nghiệm của hệ phương trình :
\(\hept{\begin{cases}ax-3=-3x+2\\y=ax-3\end{cases}}\)mà (1 ) cắt (1') tại điểm có tung độ bằng 5 => y =5 => Ta có : \(\hept{\begin{cases}ax-3=-3x+2\\5=ax-3\end{cases}\Leftrightarrow\hept{\begin{cases}a.\frac{8}{a}-3=-3.\frac{8}{a}+2\\x=\frac{8}{a}\end{cases}}\Leftrightarrow a=-8}\)
Đúng 0
Bình luận (0)
1) xác định đồ thị hàm số bậc nhất \(y=ax+b\) trong mỗi trường hợp sau:
a) đồ thị hàm số đi qua A(-1; 2), B(2; -3)
b) đồ thị hàm số có hệ số góc là 2 và cắt trục tung tại điểm có tung độ là 2
c) đồ thị hàm số tạo với trục hoành 1 góc \(60^0\) và đi qua điểm B(1; -3)
giúp mk vs ah mk cần gấp
Bài 2:
a)Xác định hàm số bậc nhất y=ax +b biết đồ thị hàm số đi qua điểm M(2;3) và song song với đường thẳng y=2x+3
b) Xác định giao điểm của đồ thị hàm số vừa tìm đc ở câu a với đồ thị hàm số y=-x+5 bằng tính toán
Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:
a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5.
b) a = 3 và đồ thị của hàm số đi qua điểm A(2; 2)
c) Đồ thị của hàm số song song với đường thẳng y = √3 x và đi qua điểm B(1; √3 + 5 ).
a) Với a = 2 hàm số có dạng y = 2x + b.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5 khi đó tung độ bằng 0 nên:
0 = 2.1,5 + b => b = -3
Vậy hàm số là y = 2x – 3
b) Với a = 3 hàm số có dạng y = 3x + b.
Đồ thị hàm số đi qua điểm (2; 2), nên ta có:
2 = 3.2 + b => b = 2 – 6 = - 4
Vậy hàm số là y = 3x – 4
c) Đường thẳng y = ax + b song song với đường thẳng y = √3 x nên a = √3 và b ≠ 0. Khi đó hàm số có dạng y = √3 x + b
Đồ thị hàm số đi qua điểm (1; √3 + 5) nên ta có:
√3 + 5 = √3 . 1 + b => b = 5
Vậy hàm số là y = √3 x + 5
Đúng 0
Bình luận (0)