Cho hình bình hành ABCD. Biết I (7/2;5/2) là trung điểm của cạnh CD, D (3;3/2) và đường phân giác góc BAC có phương trình là d: x-y+1=0. Xác định tọa độ đỉnh B.

Những câu hỏi liên quan
Cho hình bình hành ABCD có
B
^
120
0
, AB 2BC. Gọi I là trung điểm CD, K là trung điểm của AB. Biết chu vi hình bình hành ABCD bằng 60cm. Tính diện tích hình bình hành ABCD A.
100
3
c
m
2
B.
100
c
m
2
C.
200
3
c
m...
Đọc tiếp
Cho hình bình hành ABCD có B ^ = 120 0 , AB = 2BC. Gọi I là trung điểm CD, K là trung điểm của AB. Biết chu vi hình bình hành ABCD bằng 60cm. Tính diện tích hình bình hành ABCD
A. 100 3 c m 2
B. 100 c m 2
C. 200 3 c m 2
D. 200 c m 2
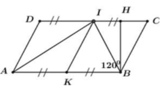
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Cho hình bình hành ABCD có AB = 6cm, BC = 10cm. Tính diện tích hình bình hành ABCD biết chiều cao tương ứng với đáy AB bằng trung bình cộng của 2 cạnh bên hình bình hành
Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)
Đúng 3
Bình luận (0)
cho hình bình hành ABCD. Lấy điểmE trên BC sao cho BE=1/3BC. F là Trung Điểm CD. Cc1 tia AE, AF lần lượi cắt đường chéo BD tại I và K. Tính diện tích tam giác AIK biết diện tích hình bình hành ABCD là 48 cm2.
Bài 7. Hình vẽ bên gồm hình chữ nhật ABCD và hình bình hành ABMN. Biết chu vi hình chữ nhật ABCD là 84m, chiều dài hơn chiều rộng 6m. Tính diện tích hình bình hành ABMN.
Đọc tiếp
Bài 7. Hình vẽ bên gồm hình chữ nhật ABCD và hình bình hành ABMN. Biết chu vi hình chữ nhật ABCD là 84m, chiều dài hơn chiều rộng 6m. Tính diện tích hình bình hành ABMN.
Nếu là hình dưới thì đây ạ:
Nửa chu vi của hcn ABCD là: 84:2=42(m)
Nhìn hình vẽ ta thấy, CR của hcn ABCD= chiều cao của hình bình hành ABMN
=> Chiều cao của hình bình hành ABMN là:
(42-6):2=18(m)
Nhìn hình vẽ, ta thấy CD hcn ABCD=đáy của hình bình hành ABMN
=> Đáy của hình bình hành ABMN là:
42-18=24(m)
Diện tích hình bình hành ABMN là:
24x18=432(m2)
Đ/s:432m2
@Teoyewmay
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có diện tích là 9968 m2.Biết độ dài đáy là 56 m. Tính chu vi hình bình hành ABCD đó.
Chiều cao của hình bình hành abcd là:
9968 : 56 = 178 ( m)
Chu vi của hình bình hành abcd là:
(178+56) x 2 = 468 (m)
Đáp số : 468 m
Chúc Bạn Học Tốt
Chiều cao của hình bình hành là:
9968:56=178 (m)
Chu vi hình bình hành là:
(56+178) x 2 = 468 (m)
Đáp số:........
trong mặt phẳng oxy cho hình bình hành ABCD biết I(7/2;5/2)là trung điểm của CD ,D(3;3/2) và đường phân giác góc BAC có phương trình là denta: x-y+1=0,Xác định tọa độ điểm B
Áp dụng công thức trung điểm: \(\left\{{}\begin{matrix}x_C=2x_I-x_D=4\\y_C=2y_I-y_D=\dfrac{7}{2}\end{matrix}\right.\) \(\Rightarrow C\left(4;\dfrac{7}{2}\right)\)
Gọi d là đường thẳng qua C và vuông góc \(\Delta\Rightarrow d\) nhận (1;1) là 1 vtpt
Phương trình d:
\(1\left(x-4\right)+1\left(y-\dfrac{7}{2}\right)=0\Leftrightarrow x+y-\dfrac{15}{2}=0\)
Gọi E là giao điểm d và \(\Delta\Rightarrow\) tọa độ E là nghiệm:
\(\left\{{}\begin{matrix}x-y+1=0\\x+y-\dfrac{15}{2}=0\end{matrix}\right.\) \(\Rightarrow E\left(\dfrac{13}{4};\dfrac{17}{4}\right)\)
Gọi F là điểm đối xứng C qua \(\Delta\Rightarrow E\) là trung điểm CF
\(\Rightarrow\left\{{}\begin{matrix}x_F=2x_E-x_C=\dfrac{5}{2}\\y_F=2y_E-y_C=5\end{matrix}\right.\) \(\Rightarrow F\left(\dfrac{5}{2};5\right)\)
Do \(\Delta\) là phân giác BAC \(\Rightarrow F\in\) đường thẳng AB
\(\overrightarrow{CD}=\left(-1;-2\right)\), do AB song song DC nên đường thẳng AB nhận (2;-1) là 1 vtpt
Phương trình AB:
\(2\left(x-\dfrac{5}{2}\right)-1\left(y-5\right)=0\Leftrightarrow2x-y=0\)
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y+1=0\\2x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(1;2\right)\)
\(\overrightarrow{AB}=\overrightarrow{DC}=-\overrightarrow{CD}=\left(1;2\right)\Rightarrow\left\{{}\begin{matrix}x_B=x_A+1=2\\y_B=y_A+2=4\end{matrix}\right.\)
\(\Rightarrow B\left(2;4\right)\)
Đúng 1
Bình luận (0)
Cho các hình bình hành ABCD,MBCN ,AMND.Tính diện tích hình bình hành MBCN biết hình bình hành ABCD là 54cm2 và độ dài AB gấp 3 lần MB
cho hình bình hành ABCD .điểm E thuộc BC sao cho 3BE = BC, F là trung điểm của CD các tia AE AF lần lượt cắt BD tại I,K .tính diện tích tam giác AIK biết diện tích hình bình hành ABCD là 48
Bạn tham khảo ở đây nhé!
http://diendan.hocmai.vn/showthread.php?t=234169
Đúng 0
Bình luận (0)



















