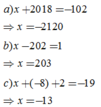Ba số nguyên dương x;y;z thỏa mãn x < y < z và tổng các nghịch đảo của chúng bằng 1 là ( x ; y ; z ) = ..............

Những câu hỏi liên quan
Tìm số nguyên x, biết:
a) x+2018 là số nguyên âm lớn nhất có ba chữ số khác nhau.
b) x-202 là số nguyên dương nhỏ nhất.
c) Tổng của ba số x; -8; 2 bằng -19.
Tìm cặp số nguyên dương (x,y) với x là số nguyên dương nhỏ nhất có ba chữ số và thỏa mãn phương trình:
\(3x^3-2y^2+4xy-8x+5128=0\)
Trong các trường hợp sau trường hợp nào cho kết quả là một số nguyên âm?
1) Tích của hai số nguyên âm và một số nguyên dương.
2) Tích của ba số nguyên âm và một số nguyên dương.
3) Tích của 2 số nguyên âm và ba số nguyên dương.
4) Tích của một số nguyên âm và hai số nguyên dương
2) Tích của ba số nguyên âm và một số nguyên dương.
4) Tích của một số nguyên âm và hai số nguyên dương
Chọn 2) và 4)
Đúng 0
Bình luận (0)
A)Giải thích vì sao mọi Số nguyên âm đều nhỏ hơn số nguyên dương
B)Tìm số nguyên dương nhỏ nhất có ba chữ số. Số nguyên âm nhỏ nhất có ba chữ số?
a) vì số nguyên âm nhỏ hơn 0,số nguyên dương lớn hơn 0
b)100 và (-999)
a. Giải thích vì sao mọi số nguyên âm đều nhỏ hơn số nguyên dương.
-- > Mọi số nguyên âm đều nhỏ hơn số nguyên dương vì số nguyên âm nhỏ hơn 0 còn số nguyên dương lớn hơn 0.
b. Tìm số nguyên dương nhỏ nhất có ba chữ số. Số nguyên âm nhỏ nhất có ba chữ số?
-- > Số nguyên dương nhỏ nhất có ba chữ số là 100.
Số nguyên âm nhỏ nhất có ba chữ số là (-999).
Tính tổng ba số nguyên dương x, y, z biết x+y+z=x*y*z.
Cho x,y,z là ba số nguyên dương nguyên tố cùng nhau t/m 1/x+1/y=1/z. Hỏi x+y có là số chính phương không? Vì sao?
#) Giải
Giả sử tồn tại x, y, z thỏa mãn đk đầu bài => 1 / x + 1 / y = 1 / z (x, y, z ≠ 0)
=> z(x + y) = xy
Không thể có |z| > 1 vì lúc đó z có ít nhất 1 ước nguyên tố p ≥ 2 => p phải là ước của x hoặc y, vô lý vì (x, z) = (y, z) = 1. Vậy z = -1, 1
Với z = -1 => -(x + y) = xy => (x + 1)(y + 1) = 1 => x + 1 = -1, y + 1 = -1
=> x = y = -2 => x, y có chung ước 2, vô lý vì (x, y) = 1
Với z = 1 => x + y = xy => (x - 1)(y - 1) = 1
=> x - 1 = 1 và y - 1 = 1 => x = y = 2, vô lý vì (x, y) = 1
Vậy không tồn tại x, y, z thỏa đk bài toán
~ Hok tốt ~
Đúng 0
Bình luận (0)
kham khảo ở đây nha
Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
vào thống kê hỏi đáp của mình nhấn zô chữ xanh trong câu trả lời này
hc tốt ~:B~
Đúng 0
Bình luận (0)
Giả sử tồn tại x, y, z thỏa mãn đk đầu bài => 1 / x + 1 / y = 1 / z (x, y, z ≠ 0)
=> z(x + y) = xy
Không thể có |z| > 1 vì lúc đó z có ít nhất 1 ước nguyên tố p ≥ 2 => p phải là ước của x hoặc y, vô lý vì (x, z) = (y, z) = 1. Vậy z = -1, 1
Với z = -1 => -(x + y) = xy => (x + 1)(y + 1) = 1 => x + 1 = -1, y + 1 = -1
=> x = y = -2 => x, y có chung ước 2, vô lý vì (x, y) = 1
Với z = 1 => x + y = xy => (x - 1)(y - 1) = 1
=> x - 1 = 1 và y - 1 = 1 => x = y = 2, vô lý vì (x, y) = 1
Vậy không tồn tại x, y, z thỏa đk bài toán hay x+y không phải số chính phương
nguồn : Câu hỏi của Quân Đặng - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Tìm bộ ba số nguyên dương x,y,z thõa mãn phương trình x+yz=2020 và xy+z=2021
Trừ vế cho vế:
\(xy+z-\left(x+yz\right)=1\)
\(\Leftrightarrow x\left(y-1\right)-z\left(y-1\right)=1\)
\(\Leftrightarrow\left(x-z\right)\left(y-1\right)=1\)
Do \(y\) nguyên dương \(\Rightarrow y\ge1\Rightarrow y-1\ge0\Rightarrow x-z>0\)
\(\Rightarrow\left\{{}\begin{matrix}x-z=1\\y-1=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=2\\z=x-1\end{matrix}\right.\)
Thế vào \(x+yz=2020\)
\(\Rightarrow x+2\left(x-1\right)=2020\)
\(\Leftrightarrow3x=2022\Rightarrow x=674\Rightarrow z=673\)
Vậy \(\left(x;y;z\right)=\left(674;673;2\right)\)
Đúng 0
Bình luận (0)
Cho 2020 số nguyên trong đó tích ba số nguyên bất kỳ là 1 số nguyên dương . CMR tất cả 2020 số nguyên đó đều là số nguyên dương
Ta có nhận xét rằng: Tích của ba số nguyên bất kỳ là một số dương thì trong đó phải tồn tại một số dương.
Do tích của 3 số nguyên bất kỳ trong 25 số đều là số dương nên ta lấy nhóm 3 số bất kỳ và lấy số dương trong đó ra.
Vậy còn lại 24 số.
Ta chia 24 số này thành 8 nhóm, mỗi nhóm có 3 số.
Vì tích của 3 số nguyên bất kì trong 24 số đó đều dương nên mỗi nhóm, ta đều lấy ra được số một dương.
Vậy thì ta được 8 số dương. Vậy còn lại 24 - 8 = 16 số.
Ta lại lấy một nhóm 3 số bất kỳ, lấy số dương trong đó. Vậy còn lại 16 - 1 = 15 số.
Lại chia 15 số thành 5 nhóm, mỗi nhóm 3 số. Tiếp tục lấy đi 1 số dương trong mỗi nhóm, ta được 5 số.
Ta còn 15 - 5 = 10 số.
Ta lại lấy một nhóm 3 số bất kỳ, lấy số dương trong đó. Vậy còn lại 10 - 1 = 9 số.
Lại chia 9 số thành 3 nhóm 3 số. Tiếp tục lấy đi 3 số dương trong 3 nhóm.
Ta còn 9 - 3 = 6 số.
Ta chia 6 số thành 2 nhóm, tiếp tục lấy đi 2 số dương, ta còn 4 số.
Lấy nhóm 3 số bất kì, chọn được số dương trong đó.
Vậy còn 3 số.
Trong 3 số này lấy một số dương. Vậy chỉ còn 2 số.
Tích hai số này là số dương nên hoặc chúng cùng âm, cùng dương.
Nếu chúng cùng âm, ta lấy 2 số dương bất kì vừa chọn được trong 23 số kia nhân với một trong hai số đã cho thì được tích âm.
Vậy vô lý.
Từ đó suy ra hai số còn lại cùng dương.
Nói cách khác cả 25 số đều là số dương.
:D
Đúng 0
Bình luận (0)
Câu hỏi của Nguyễn Tuyết Mai - Toán lớp 6 - Học toán với OnlineMath
Em tham khảo lời giải bài tương tự tại đây nhé.
Đúng 0
Bình luận (0)
Ta có:A= (n-1)n(n+1) chia hết cho 504
Ta có: 504=32.7.832.7.8 ; Đặt n=a3a3, cần chứng minh
A=(a3−1)a3(a3+1)(a3−1)a3(a3+1) chia hết cho 504
*Nếu a chẵn thì a3a3 chia hết cho 8; nếu a lẻ thì a3−1a3−1 và a3+1a3+1 là 2 số chẵn liên tiếp nên (a3−1)(a3+1)(a3−1)(a3+1) chia hết cho 8 \Rightarrow mọi trường hợp A đều chia hết cho 8
* Nếu a chia hết cho 7 thì A chia hết cho 7. Nếu a ko chia hết cho 7 thì (a3−1)(a3+1)(a3−1)(a3+1)= a6−1a6−1 chia hết cho 7
*Nếu a chia hết cho 3 thì a^3 chia hết cho 9. Nếu a= 3k+1 hoặc a=3k-1 thì a3a3 = 27k3+27k2+9k+127k3+27k2+9k+1 hoặc a3=27k3−27k2+9k−1a3=27k3−27k2+9k−1, nên a3+1a3+1hoặc a3−1a3−1 sẽ có 1 số chia hết cho 9
\Rightarrow A chia hết cho 7,8,9
\Rightarrow A chia hết cho 504
Đúng 0
Bình luận (0)
ba số nguyên dương x < y < z thỏa mãn 1/x + 1/y + 1/z = 1 là.....
tìm ba số nguyên dương x,y,z thỏa mãn x+y+z+xy+yz+zx chia hết cho xyz