Cho tam giác ABC . Các tia phân giác góc B,C cắt nhau ở I .
Tính góc BTC biết:
a) Góc B = 80o ; góc C = 40o
b) Góc A = 80o
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính ∠(BIC) biết rằng: ∠B = 80o,∠C = 40o
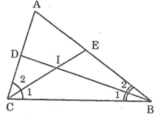
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính ∠(BIC) biết rằng:
∠A = 80o
∠A = mo
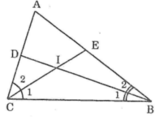
Ta có:
+ Trong ΔBIC có ∠BIC = 180o - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠ABC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠ABC + ∠ACB) (2)
⇒ ∠ABC + ∠ACB = 180 - ∠A (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180o - 1/2.(180 - ∠A) = 90o + 1/2.∠A
+) Nếu ∠A = 80o ⇒ ∠BIC = 90º + 1/2.80o = 130o.
+) Nếu ∠A = mo ⇒ ∠BIC = 90o + 1/2.mo.
Cho \(\Delta ABC\) có góc A = a. Các tia phân giác của các góc B và C cắt nhau ở I. Các tia phân giác của góc ngoài đỉnh B và C cắt nhau ở K. Tia phân giác của góc B cắt tia phân giác của góc ngoài đỉnh C ở E.
Tính số đo góc BTC
Cho tam giác ABC có ∠ A = 80 o , hai tia phân giác của góc B và C cắt nhau tại I.
b.Giả sử góc ∠ B = 30 o . So sánh các cạnh của tam giác ABC
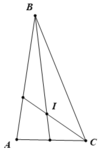
b. Khi ∠B = 30o thì ∠C = 180o - 30o - 80o = 70o ( 1 điểm )
Vì ∠B < ∠C < ∠A ⇒ AC < AB < BC ( 1 điểm )
B. Phần tự luận (6 điểm)
Cho tam giác ABC có ∠ A = 80 o , hai tia phân giác của góc B và C cắt nhau tại I.
a. Tính góc( BIC)
a. Hình vẽ ( 0.5 điểm )
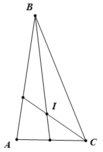
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )
B. Phần tự luận (6 điểm)
Cho tam giác ABC có ∠ A = 80 o , hai tia phân giác của góc B và C cắt nhau tại I.
a. Tính góc( BIC)
a. Hình vẽ ( 0.5 điểm )
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )
Cho tam giác ABC có góc A = 60 độ. Các tia phân giác của góc B và góc C cắt nhau ở I. các tia phân giác ngoài của góc B và góc C cắt nhau ở K. Tia phân giác góc B cắt tia phân giác góc ngoài ở đỉnh C tại E. Tính góc BIC, BKC, BEC.
Cho tam giác ABC có góc A bằng 60 độ. Các tia phân giác của góc B và góc C cắt nhau ở I. Các tia phân giác ngoài của góc B và góc C cắt nhau ở K. Tia phân giác góc B cắt tia phân giác ngoài ở đỉnh C tại E. Tính góc BIC, BKC, BEC
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
⇒ góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
⇒ góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
Ai trên 10 điểm hỏi đáp thì mình nha mình đang cần gấp chỉ còn 99 điểm là tròn rồi mong các bạn hỗ trợ mình sẽ đền bù xứng đáng
Cho tam giác ABC có góc A= 60 độ. Các tia phân giác của góc B và góc C cắt nhau ở I. Các tia phân giác ngoài của goác B và C cắt nhau ở K. Tia phân giác góc B cắt tia phân giác góc ngoài ở đỉnh C tại E. Tính góc BIC, BKC, BEC.