Cho góc xOy. Trên tia Ox lấy hai điểm A ; B . ( A nằm giữa O và B ) ; Trên tia Oy lấy hai điểm C và D ( C nằm giữa O và D ) sao cho AB = CD . Gọi E ; F lần lượt là trung điểm của AC và BD . CMR : EF song song với tia phân giác góc xOy .

Những câu hỏi liên quan
Cho góc xOy nhọn. Lấy điểm A trên tia Ox, điểm B trên tia Oy. Trên tia Ox lấy điểm C sao cho BC là tia phân giác của góc ABy. Gọi I là giao điểm của hai tia phân giác góc xAB và xOy. Chứng minh ba điểm B, I, C thẳng hàng.
Góc AIB = 180 độ - 1/2 BAC - ABI
Góc AIC = 180 độ - 1/2 BAC - ACI
⇒ AIB + AIC = 180 độ - BAC - (ABI + ACI)
Giả sử B, I, C thẳng hàng
⇒BIC = 180 độ = AIB + AIC
→360 độ - BAC - (ABI + ACI) = 180 độ
ABI + ACI = 180 độ - BAC (LĐ)
Vậy điều giả sử là đúng
⇒B, I, C thẳng hàng
Đúng 0
Bình luận (0)
Bài 7. Cho góc xOy nhọn. Lấy điểm A trên tia Ox, điểm B trên tia Oy. Trên tia Ox lấy điểm C sao cho BC là tia phân giác của góc ABy. Gọi I là giao điểm của hai tia phân giác góc xAB và xOy. Chứng minh ba điểm B, I, C thẳng hàng
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
Tia OI là tia phân giác của góc xOy.
Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
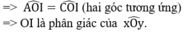
Đúng 0
Bình luận (0)
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B, D sao cho OA OB, OC OD.
a) Chứng minh: AD BC.
b) Gọi E là giao điểm AD và BC. Chứng minh OE là tia phân giác của góc xOy
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B, D sao cho OA = OB, OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh OE là tia phân giác của góc xOy
Cho góc xOy khác góc bẹt. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB. Qua điểm A, kẻ đường thẳng a vuông góc với Ox. Qua điểm B , kẻ đường thẳng b vuống góc với Oy. Hai đường thẳng cắt nhau tại C. Chứng minh rằng:
a) CA=CB
b) OC là tia phân giác của góc xOy
Cho góc nhọn xoy. Trên tia ox lấy hai điểm A,C trên tia ít lấy hai điểm B,D sao cho OA=OB , OC=OD.a) chứng minh AD=BC. b) gọi e là giao điểm AD và BC chứng minh OE là tia phân giác của góc XOY. Vẽ hình
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B, D sao cho OA = OB, OC = OD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh OE là tia phân giác của góc xOy
a) Xét \(\Delta AOD\)và \(\Delta\)BOC có:
OA=OB (gt)
\(\widehat{O}\)chung
OD=OC (gt)
=> \(\Delta AOD=\Delta BOC\left(cgc\right)\)
=> AD=BC (2 cạnh tương ứng) (đpcm)
b) Ta có: \(\hept{\begin{cases}OC=OD\\OA=OB\end{cases}\Rightarrow OC-OA=OD-OB\Leftrightarrow AC=BD}\)
Xét tam giác EBD và tam giác EAC có:
AC chung
\(\widehat{DBE}=\widehat{CAE}\)
\(\widehat{BDE}=\widehat{ECA}\)
\(\Rightarrow\Delta EBD=\Delta EAC\left(gcg\right)\)
=> DE=EC (2 cạnh tương ứng)
Xét tam giác OED và tam giác OEC có:
OD=OC (gt)
OE chung
DE=EC (cmt)
=> \(\Delta OED=\Delta OEC\left(ccc\right)\)
=> \(\widehat{DOE}=\widehat{COE}\)(2 góc tương ứng)
=> OE là phân giác \(\widehat{xOy}\)(đpcm)
Cho 2 góc kề bù xOy và yOz. Trên tia Oy lấy điểm A, trên tia Ox lấy điểm B, trên tia AD lấy điểm C sao cho AB
a,Tia Ox có nằm giữa hai tia OA và OC không? Vì sao ?
b,Cho góc yOz =1300 ; góc zOc = 1500 . Tính số đo góc AOC
Cho góc nhon xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC=OD.
a) Chứng minh: AD=BC
b) Gọi E là giao điểm AD và BC. Chứng minh: OE là tia phân giác của góc xOy
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C. Trên tia Oy lấy hai điểm B,D sao cho OA = OB, AC = BD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh: ΔEAC = ΔEBD
c) Chứng minh: OE là phân giác của góc xOy, OE vuông góc CD
















