Dpcm ANx // CNy 
do AB//CD nen 
=>AM // CM va MB//ND 
=>AMB // CND 
=>ANx // CNy

a). Ta có: góc AMx=góc B (GT)

        Mà góc AMx và góc B là hai góc đồng vị.

=> Mx//BC.

Kéo dài tia Mx, cắt CD tại E.

Vì AB//CD(gt) nên AMEˆ=DEMˆ(slt)AME^=DEM^(slt)

mà theo gt AMEˆ=CNyˆAME^=CNy^ nên DEMˆ=CNyˆDEM^=CNy^

=> Mx//Ny(do có 1 cặp góc bằng nhau ở vị trí so le trong

do AB//CD nen 
=>AM // CM va MB//ND 
=>AMB // CND 
=>ANx // CNy 

Vì AB//CD

=>AM//CM;MB//ND

=>AMB//CND

=>ANx//CNy

Vậy ANx//CNy

Giải:

Do AB // CD nên: \(\widehat{AMN}+\widehat{MNC}=180^o\) ( 2 góc trong cùng phía bù nhau )

\(\Rightarrow\widehat{AMx}+\widehat{xMN}+\widehat{MNC}=180^o\)

Do \(\widehat{AMx}=\widehat{CNy}\left(gt\right)\)

\(\Rightarrow\widehat{CNy}+\widehat{xMN}+\widehat{MNC}=180^o\)

\(\Rightarrow\left(\widehat{CNy}+\widehat{MNC}\right)+\widehat{xMN}=180^o\)

\(\Rightarrow\widehat{MNy}+\widehat{xMN}=180^o\)

Mà 2 góc \(\widehat{MNy},\widehat{xMN}\) ở vị trí trong cùng phía

\(\Rightarrow\)Mx // Ny ( đpcm )

Vậy...

ê bạn Nguyễn Huy Tú ơi bạn có nick ở hh à

Mình thích những người nào vừa có tên hay lại vừa hok giỏi như bạn đó. Add friend fb ko??? Sau này bạn làm giáo sư tiến sĩ j đó mik còn đc nhờ. Iu bạn! ( tên nick này ko phải tên thật của mik. Mik là con gái bạn ạ. Bạn đòng ý add friend thì mik khai tên ra cho)😀😀😀

Dpcm ANx // CNy 
do AB//CD nen 
=>AM // CM va MB//ND 
=>AMB // CND 
=>ANx // CNy 

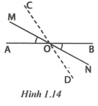
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^  mà A O M ^ = B O N ^  (hai góc đối đỉnh) nên M O C ^ = D O N ^ .

Ta có M O D ^ + D O N ^ = 180 °  (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .

Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 °  nên hai tia OC, OD đối nhau.

Ÿ Chứng tỏ một tia là tia phân giác