Cho tam giác ABC. Các đường trung tuyến BD; CE. Gọi M; N theo thứ tự là trung điểm của BE; CD. Gọi I; K theo thứ tự là giao điểm của MN với BD; CE. Chứng minh MI = IK = KN
Những câu hỏi liên quan
Cho tam giác ABC cân tại A, vẽ trung tuyến AM và đường phân giác BD. Xác định các góc tam giác ABC biết BD = 2AM
từ M vẽ MK// BD ( K thuộc AC )
Tam giác BDC có : M là trung điểm BC; MK//BD
Suy ra : K là trung điểm CD
Do đó: MK là đường trung bình của tam giác BDC.
--> MK = BD/2 = 2AM/2 = AM
---> tam giác AMK cân tại M --> góc MAK = góc MKA
Ta có : góc MAK + góc C = 90 độ
hay góc MKA + góc C = 90 độ
==> góc MKA = 90 độ - góc C (1)
Lại có : góc MKA = góc KMC + góc C = góc DBC + góc C = góc B/2 + góc C = góc C/2 + góc C = 3/2. góc C (2)
Từ (1) (2) ==> 90 độ - góc C = 3/2. góc C
==> 5/2. góc C = 90 độ
==> góc C = 36 độ
==> góc B = 36 độ
==> góc A= 180-36.2=108 độ
Đúng 0
Bình luận (0)
B1.Cho tam giác ABC có BC=10cm .Các đường trung tuyến BD=9cm và CE=12cm.
CM \(BD\perp CE\)
B2. Cho tam giác ABC có độ dài các đường trung tuyến AM=15cm; BD=9cm;CE=12cm.
Tính độ dài các cạnh của tam giác ABC
mọi người ai giúp mình vs giải chi tiết nha
Cho tam giác ABC, M là trung điểm của BC. Trên tia AM lấy điểm D sao cho trọng tâm G là trung điểm AD.
a, So sánh các cạnh GD và cạnh BD của tam giác BGD với các đường trung tuyến của tam giác ABC
b, So sánh các đường trung tuyến của tam giác BGD với các cạnh AB và AC của tam giác ABC
Cho tam giác ABC cân tại A, có AM là đường trung tuyến, BD phân giác góc B, biết BD=2AM, tính các góc trong tam giác ABC
1.Tam giác ABC vuông tại A có trung tuyến AM vuông góc với trung tuyến BN, cho AB = x. Tính AC, BC theo x?
2. Tam giác ABC vuông tại A có BD là đường phân giác, trung tuyến AM vuông góc BD. Cho BD = \(2\sqrt{3}x\)(x>0). Tính độ dài các cạnh của tam giác ABC?
cho tam giác ABC, M trung điểm BC. trên tia AM lấy điểm D sao cho trọng tâm G là trung điểm AD
a) so sánh các cạnh GD và cạnh BD của tam giác BGD với các đường trung tuyến của tam giác ABC
b) so sánh các đường trung tuyến cuẩ tam giác BGD với các cạnh AB và AC cùa tam giác ABC
Cho tam giác ABC có BC = 34 cm, đường trung tuyến BD = 24 cm, đường trung tuyến CE = 45 cm. Gọi G là giao điểm của BD và CE. Tính độ dài các cạnh của tam giác GDE
G là giao điểm của 2 đường trung tuyến BD và CE
Suy ra : G là trọng tâm tam giác ABC
Suy ra :
GD = 1/3 BD = 1/3 x 24 = 8 ( cm )
GE = 1/3 CE = 1/3 x 45 = 15 ( cm )
Xét tam giác ABC có :
E là trung điểm AB ( trung tuyến CE )
D là trung điểm AC ( trung tuyến BD )
Suy ra : ED là đường trung bình của tam giác ABC
Suy ra ED : = 1/2 x BC = 1/2 x 34 = 17 ( cm )
Vậy GD = 8 cm
GE = 15 cm
ED = 17 cm
cho tam giác ABC có BC=34cm đường trung tuyến BD=24cm ,đường trung tuyến CE=45cm,G là giao điểm của 2 đường trung tuyến BD và CE.tính chu vi tam giác GDE
Cho tam giác ABC, các đường trung tuyến BD, CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC. Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì?
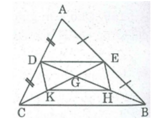
Nếu BD ⊥ CE ⇒ DH ⊥ EK
Hình bình hành DEHK có hai đường chéo vuông góc nên nó là hình thoi.
Đúng 0
Bình luận (0)
Cho tam giác abc có bd là đường trung tuyến. trong tam giác abd vẽ các trung tuyến am và bm cắt nhau tại h: a, cm dh//bc b,dh=bc/3