tính diện tích hình thang ABCD có đường cao 12 cm, hai đường chéo AC; BD vuông góc với nhau và BD =15 cm

Những câu hỏi liên quan
Câu 11.11. Tính diện tích hình thang ABCD, có đường cao bằng 12 cm, hai đường chéo AC và BD vuông góc với nhau, DB = 15 cm.
Câu 11.12. Hình thang cân ABCD có đáy lớn CD = 10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tìm đường cao của hình thang
Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),
Cho hình thang ABCD (AB // CD) có hai đường chéo vuông góc với nhau. Đường cao là 12 cm, đường chéo BD là 15 cm. Tính diện tích hình thang ABCD.
Cho hình thang ABCD có đường cao dài 12 cm,hai đường chéo AC và BD vuông góc với nhau,BD=15 cm.Tính diện tích hình thang ABCD ?
Cho hình thang ABCD có hai đáy AB = 5cm, CD = 15 cm và hai đường chéo là AC = 16 cm, BD = 12 cm. Tính diện tích hình thang ABCD
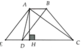
Qua A kẻ AE//BD (E Î DC)
Þ AE = BD = 12cm, DE = AB = 5cm
Þ DAEC vuông tại A (định lý Pytago đảo)
⇒ A H = A E . A C E C = 12.16 20 = 9 , 6 c m
Þ SABCD = 96cm2
Đúng 0
Bình luận (0)
cho hình thang ABCD đáy AD và BC hai đường chéo AC ,BD cắt nhau tại điểm M .tính diện tích hình MAB,MBC,MCD,MDA biết rằng AD=20 cm,BC=10cm và đường cao hình thang là 12 cm
Cho hình thang ABCD ( AB // CD ) có hai đường chéo vuông góc, BD =15 cm, AC = 20 cm.
a) Tính diện tích hình thang.
b) Tính chiều cao của hình thang.
Tính diện tích hình thang ABCD có đường chéo AC=9cm; BD =12 cm và tổng hai đáy AB+CD= 15 cm.
Cho hình thang ABCD có AB // CD , AD = 12 cm , CD = 16 cm . Góc A = góc D = 90 độ , hai đường chéo AC vuông góc với BD tại O . Tính diện tích ABCD
Cho hình thang ABCD ( đáy lớn AD , đáy bé BC ) hai đường chéo AC và BD cắt nhau tại điểm O . Tính diện tích hình tam giác BOC , biết rằng AD = 18 cm , BC = 12 cm và chiều cao của hình thang là 15 cm
ak cái này biết = 36
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%
tk nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang ABCD có hai đáy là AB và CD. Biết AB = 15 cm , CD = 20 cm;
chiều cao hình thang là 14cm. Hai đường chéo AC và BD cắt nhau ở E .
a) Tính diện tích hình thang ABCD.
b) Tính diện tích tam giác CED.
c) Chứng minh hai tam giác AED và BEC có diện tích bằng nhau.
mỗi cái S là diện tích
a, diện tích hình thang ABCD là: (15+20).142=245(cm2)(15+20).142=245(cm2)
b,BEDE=SAEBSAED=SCEBSCED=SAEB+SCEBSAED+SCED=SABCSACD=ABCD=34BEDE=SAEBSAED=SCEBSCED=SAEB+SCEBSAED+SCED=SABCSACD=ABCD=34
⇒SCEBSCED=34⇒SCEB+SCEDSCED=74⇒SDBCSCED=74⇒SCEBSCED=34⇒SCEB+SCEDSCED=74⇒SDBCSCED=74
⇒SCED=47.SDBC⇒SCED=47.SDBC
SDBC=20.142=140(cm2)SDBC=20.142=140(cm2)
⇒SCED=47.140=80(cm2)⇒SCED=47.140=80(cm2)
c,SAED=SACD−SECDSAED=SACD−SECD
SBEC=SBCD−SECDSBEC=SBCD−SECD
MÀ SACD=SBCD⇒SAED=SBEC
Xem thêm câu trả lời

















