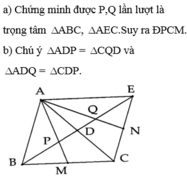
Cho tam giác ABC. Vẽ trung tuyến BD. Trên tia đối của tia BD lấy E sao cho DE=BD. Gọi M ; N là thứ tự trung điểm của BC và CE. Gọi I ; K thứ tự là giao điểm của AM ; AN với BE. Chứng minh BI = IK = KE

Những câu hỏi liên quan
cho tam giác ABC, đường trung tuyến BD. Trên tia đối của BD lấy E sao cho DE=DB. Gọi M, N lần lượt là trung điểm của BC và EC. Gọi P, Q lần lượt là giao điểm của AM, AN với BE. CMR BP=PQ=QE2cho tam giác ABC, đường trung tuyến BD. Trên tia đối của BD lấy E sao cho DE=DB. Gọi M, N lần lượt là trung điểm của BC và EC. Gọi P, Q lần lượt là giao điểm của AM, AN với BE. CMR BP=PQ=QE
Cho tam giác ABC , BD là đường trung tuyến . Trên tia đối của tia BD lấy điểm E sao cho DE=BD. Gọi M,N lần lượt là trung điểm cua BC và EC. Gọi P,Q lần lượt là giao điểm của AM,AN với BE. CM: BP=PQ=QE
cho tam giác abc vuông tại a đường cao ah đường trung tuyến am gọi d là điểm trung điểm của ab trên tia đối của tia mb lấy điểm e sao cho bd = de chứng minh m và e đối xứng qua ab
Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE=BD. Gọi M,N theo thứ tự là trung điểm BC,CE. Gọi I, K theo thứ tự là giao điểm của AM,AN với BE. Chứng minh BI=IK=KE
cho tam giác ABC. Đường trung tuyến BD. Trên tia đối của tia BD lấy điểm E sao cho DE= BD. Gọi M.N theo thứ tự là trung điểm của BD và CE. Gọi I và K theo thứ tự là giao điểm của AM và AN với BE .
CMR :BI = IK = KE
Cho tam giác ABC , đường trung tuyến BD . Trên tia đối của tia DB lấy điểm E sao cho DE = BD Gọi M , N theo thứ tự là trung tuyến BC, CE . Gọi I và K theo thứ tự là giao điểm của AM , AN với BE . Chứng minh rằng BI = IK = KE
Câu hỏi của Lê Thanh Phúc - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo ở link này nhé.
Đúng 0
Bình luận (0)
Bạn có thể tham khảo link này:
https://h.vn/hoi-dap/question/216158.html
.
1 / Cho tam giác ABC có BC = 10cm . Các đường trung tuyến BD và CE có độ dài theo thứ tự là 9cm và 12cm .Cm : BD vuông góc CE
2 / Cho tam giác ABC ,đường trung tuyến BD . Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi M và N lần lượt là trung điểm của BC và CE . Gọi I , K theo thứ tự giao điểm của AM , AN với BE . Chứng minh rằng : BI = IK = KE
1.gọi giao của BD và CE là O
ta có: OB=2/3 BD=> OB=2/3 x 9=6
ta có: OC=2/3 EC=> OC=2/3 x12=8
ta có:\(OC^2+OB^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
=> tam giác OBC vuông tại O=> BD_|_CE tại O
Đúng 0
Bình luận (0)
1.gọi giao của BD và CE là O
ta có: OB=2/3 BD=> OB=2/3 x 9=6
ta có: OC=2/3 EC=> OC=2/3 x12=8
ta có:$OC^2+OB^2=6^2+8^2=36+64=100$OC2+OB2=62+82=36+64=100
$BC^2=10^2=100$BC2=102=100
=> tam giác OBC vuông tại O=> BD_|_CE tại O
Đúng 0
Bình luận (0)
Cho tam giác ABC, đường trưng tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi P, Q lần lượt là điểm trên BE sao cho BP = PQ = QE. Chứng minh:
a) CP, CQ cắt AB, AE tại trung điểm của AB,AE.
b) CP//AQ và CQ//AP.
cho tam giác ABC cân tại A .trên tia đối BA lấy điểm D , trên tia đói CA lấy điểm E sao cho BD=CE . BD cắt DE tại M . cmr M là trung điểm của DE