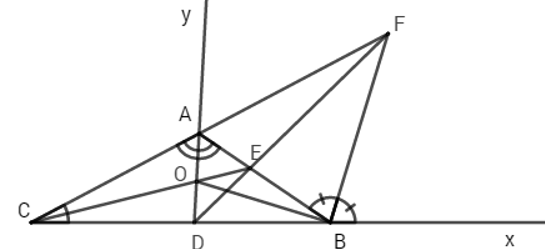
Cho tam giác ABC có góc A=120 độ, phân giác AD lần lượt cắt AB; AC ở E và F. Trên EB và FC lấy các điểm K và I sao cho EK=FI
a) Chứng minh tam giác DEF đều
b) Chững minh tam giác DIK cân
c) Từ C kẻ đường thẳng song song với AD cắt tia BA tại M
Chứng minh tam giác MAC đều. Tính AD theo CM=m và CF=n