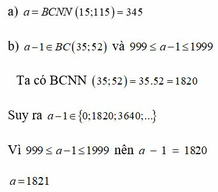Tìm a,b,c là số tự nhiên thỏa mãn: a nhỏ nhất và 7a2 - 9b2 + 29=0 ; 9b2 - 11c2 - 25 = 0.

Những câu hỏi liên quan
Tìm a,b,c là số tự nhiên thỏa mãn: a nhỏ nhất và 7a2 - 9b2 + 29=0 ; 9b2 - 11c2 - 25 = 0.
Tìm các số tự nhiên a, b, c sao cho a nhỏ nhất thỏa mãn 7a2-9b2+29=0 và 9b2-11c2-25=0
Tìm số tự nhiên :29 dư 5; :31 dư 28
a)Tìm số tự nhiên nhỏ nhất thỏa mãn
b)Tìm số tự nhiên trong khoảng từ 2000-3000 thỏa mãn
c)Các số đó chia cho 899 dư bao nhiêu
Tìm số tự nhiên M nhỏ nhất có 4 chữ số thỏa mãn : M= a+b=c+d=e+f
Biết rằng a,b,c,d,e,f là các số tự nhiên khác 0 thỏa mãn a/b = 14/22 , c/d = 11/13 , e/f = 13/17
Ta có:
\(\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k\)
\(\frac{c}{d}=\frac{11}{13}=\frac{11m}{13m}=>c=11m,d=13m=>M=c+d=11m+13m=24m\)
\(\frac{e}{f}=\frac{13}{17}=\frac{13n}{17n}=>e=13n,f=17n=>M=e+f=13n+17n=30n\)
=>M=36k=24m=30n
=>M chia hết cho 36,24,30
Ta thấy: ƯCLN(36,24,30)=360
=>M chia hết cho 360
=>M=360h
mà M là số bé nhất có 4 chữ số=>h bé nhất
=>999<360h
=>2<h
mà h bé nhất
=>h=3
=>M=3.360=1080
Vậy M=1080
Đúng 1
Bình luận (0)
$\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k$
Đúng 0
Bình luận (0)
Tìm số tự nhiên a, biết rằng:
a) a là số nhỏ nhất khác 0 thỏa mãn a ⋮ 15 và a ⋮ 115
b) a - 1 ⋮ 52 , a - 1 ⋮ 35 và 1000 < a < 2000
Tìm số tự nhiên a, biết rằng:a, a là số nhỏ nhất khác 0 thỏa mãn a chia hết cho 15 và 115b, a – 1 chia hết cho 52; a – 1 chia hết cho 35 và 1000 a 2000
Đọc tiếp
Tìm số tự nhiên a, biết rằng:
a, a là số nhỏ nhất khác 0 thỏa mãn a chia hết cho 15 và 115
b, a – 1 chia hết cho 52; a – 1 chia hết cho 35 và 1000 < a < 2000
a, a = BCNN(15;115) = 345
b, a – 1 ∈ BC(35;52) và 999 < a – 1 < 1999
Ta có BCNN(35;52) = 35.52 = 1820
Suy ra a – 1 ∈ {0;1820;3640;...}
Vì 999 < a – 1 < 1999 nên a – 1 = 1820
a = 1821
Đúng 0
Bình luận (0)
Số tự nhiên a lớn nhất thỏa mãn 75 ⋮ a và 100 ⋮ a là:
Số tự nhiên a nhỏ nhất thỏa mãn 20 ⋮ a và 35 ⋮ a là:
Có đề rùi nè các bạn ơi
a, tìm số tự nhiên nhỏ nhất có tổng các chữ số của nó bằng 21
b, tìm số tự nhiên x,y thỏa mãn : ( x + 1 ) ( 2 y + 1 ) = 29
a)cho B=88..88(có n chữ số 8) -9+n với n thuộc N* . Chứng minh B chia hết cho 9
b) tìm số tự nhiên x,y,z sao cho x nhỏ nhất thỏa mãn 7x^2 -9y^2 +29 =0 và 9y^2 - 11z^2 -25=0