Cho a , b , c là các số thực đôi 1 khác nhau thuộc [ 0 ; 2 ]
Tìm GTNN của \(P=\frac{1}{\left(a-b\right)^2}+\frac{1}{\left(b-c\right)^2}+\frac{1}{\left(c-a\right)^2}\)
Những câu hỏi liên quan
x là số thực và a,b,c là các số thực đôi một khác nhau và khác 0 thỏa mãn \(x=a+\dfrac{1}{b}=b+\dfrac{1}{c}=c+\dfrac{1}{a}\)Tính xabc
cho a,b,c là các số thực đôi 1 khác nhau và khác 0 thoả mãn: a^2-b=b^2-c=c^2-a. tính giá thị của biểu thức P=(a+b)(b+c)(c+a)
Chứng minh nếu a; b; c là các số thực đôi một khác nhau thì
\(\frac{a-b}{1+ab}+\frac{b-c}{1+bc}+\frac{c-a}{1+ca}\)khác 0
cho a,b,c là các số thực đôi một khác nhau
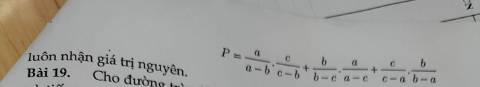
\(P=\dfrac{ab}{\left(a-c\right)\left(b-c\right)}+\dfrac{bc}{\left(b-a\right)\left(c-a\right)}+\dfrac{ca}{\left(c-b\right)\left(a-b\right)}\)
\(=\dfrac{ab\left(a-b\right)+bc\left(b-c\right)-ca\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab\left(a-b\right)+b^2c-bc^2-a^2c+ac^2}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab\left(a-b\right)-c\left(a-b\right)\left(a+b\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{ab-c\left(a+b\right)+c^2}{\left(b-c\right)\left(a-c\right)}=\dfrac{ab-bc+c^2-ca}{\left(b-c\right)\left(a-c\right)}\)
\(=\dfrac{b\left(a-c\right)-c\left(a-c\right)}{\left(b-c\right)\left(a-c\right)}=\dfrac{\left(b-c\right)\left(a-c\right)}{\left(b-c\right)\left(a-c\right)}=1\)
Đúng 0
Bình luận (0)
cho a,b,c là các số thực thỏa man: a+\(\dfrac{1}{b}=b+\dfrac{1}{c}=c+\dfrac{1}{a\backslash}\).
a) chứng minh nếu a,b,c đôi một khác nhau thì a2b2c2=1
b) chứng minh rằng nếu a,b,c>0 thì a=b=c
cho a,b,c là các số thực khác nhau đôi một và khác 0 thoã mãn:\(a^2-b=b^2-c=c^2-a\)tính gt của P=(a+b)(b+c)(c+a)
Ta có:
\(a^2-b=b^2-c=c^2-a\Rightarrow\hept{\begin{cases}a^2-b^2=b-c\\b^2-c^2=c-a\\c^2-a^2=a-b\end{cases}}\)\(\Rightarrow\hept{\begin{cases}a+b=\frac{b-c}{a-b}\\b+c=\frac{c-a}{b-c}\\c+a=\frac{a-b}{c-a}\end{cases}}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=\frac{b-c}{a-b}.\frac{c-a}{b-c}.\frac{a-b}{c-a}=1\)
Đúng 0
Bình luận (0)
tìm x,y thuộc N để 2^x+242=3^y
cho 3 số thực a,b,c khác 0 và đôi 1 khác nhau thỏa mãn: a^2 .(b+c)=b^2.(a+c)=2016. tính g.trị của biểu thức A=c^2.(a+b)
Cho a, b, x là các số thực đôi khác nhau và khác 0 thỏa mãn:
\(a+\frac{1}{b}=b+\frac{1}{c}=c+\frac{1}{a}\)
Chứng minh rằng abc= 1 hoặc abc= -1
cho 3 số khác nhau từng đôi 1 và khác 0 thõa mãn: a/b+c=b/a+c=c/a+b
Cm: b+c/a=a+c/b=a+b/c không phụ thuộc vào các giá trị của a,b,c