Bài 5: Khoảng cách
Nội dung lý thuyết
Các phiên bản khácI. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG, ĐẾN MỘT MẶT PHẲNG
1. Khoảng cách từ một điểm đến một đường thẳng
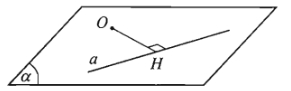
Cho điểm \(O\) và đường thẳng \(a\). Trong mặt phẳng \(\left(O,a\right)\) gọi \(H\) là hình chiếu vuông góc của \(O\) trên \(a\). Khi đó khoảng cách giữa hai điểm \(O\) và \(H\) được gọi là khoảng cách từ điểm \(O\) đến đường thẳng \(a\), kí hiệu là \(d\left(O,a\right)\).
2. Khoảng cách từ một điểm đến một mặt phẳng
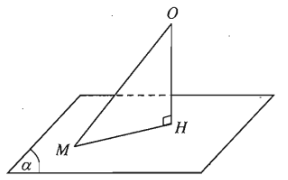
Cho điểm \(O\) và mặt phẳng \(\left(\alpha\right)\). Gọi \(H\) là hình chiếu vuông góc của \(O\) lên mặt phẳng \(\left(\alpha\right)\). Khi đó khoảng cách giữa hai điểm \(O\) và \(H\) được gọi là khoảng cách từ điểm \(O\) đến mặt phẳng \(\left(\alpha\right)\), kí hiệu là \(d\left(O;\left(\alpha\right)\right)\).
II. KHOẢNG CÁCH GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG, GIỮA HAI MẶT PHẲNG SONG SONG
1. Khoảng cách giữa đường thẳng và mặt phẳng song song
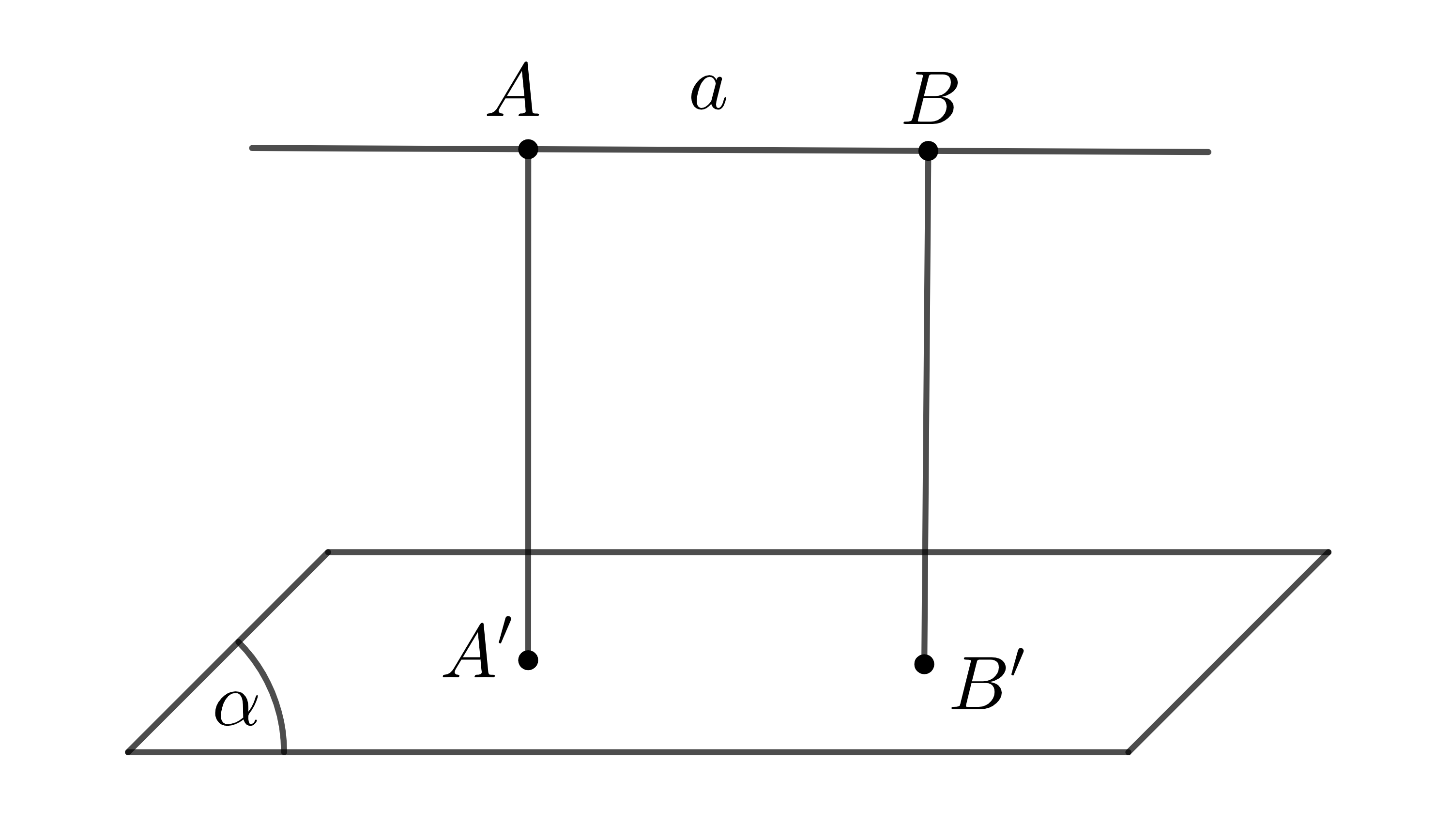
Cho đường thẳng \(a\) song song với mặt phẳng \(\left(\alpha\right)\). Khoảng cách giữa đường thẳng \(a\) và mặt phẳng \(\left(\alpha\right)\) là khoảng cách từ một điểm bất kì của \(a\) đến mặt phẳng \(\left(\alpha\right)\), kí hiệu là \(d\left(a,\left(\alpha\right)\right)\).
2. Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.
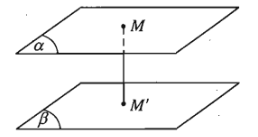
Ta kí hiệu khoảng cách giữa hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) song song với nhau là \(d\left(\left(\alpha\right),\left(\beta\right)\right)\). Khi đó \(d\left(\left(\alpha\right),\left(\beta\right)\right)=d\left(M,\left(\beta\right)\right)\) với \(M\in\left(\alpha\right)\), và \(d\left(\left(\alpha\right),\left(\beta\right)\right)=d\left(M',\left(\alpha\right)\right)\) với \(M'\in\left(\beta\right)\).
@2249912@
III. ĐƯỜNG VUÔNG GÓC CHUNG VÀ KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
1. Định nghĩa
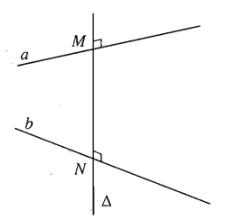
a) Đường thẳng \(\Delta\) cắt hai đường thẳng chéo nhau \(a\) và \(b\) và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của \(a\) và \(b\).
b) Nếu đường thẳng vuông góc chung \(\Delta\) cắt hai đường thẳng chéo nhau \(a\), \(b\) lần lượt tại \(M,N\) thì độ dài đoạn thẳng \(MN\) gọi là khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\).
2. Cách tìm đường vuông góc chung của hai đường thẳng chéo nhau
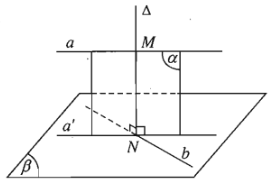
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Gọi \(\left(\beta\right)\) là mặt phẳng chứa \(b\) và song song với \(a\), \(a'\) là hình chiếu vuông góc của \(a\) trên mặt phẳng \(\left(\beta\right)\).
Gọi \(N\) là giao điểm của \(a'\) và \(b\). Gọi \(\left(\alpha\right)\) là mp chứa \(a\) và \(a'\), \(\Delta\) là đường thẳng đi qua \(N\) và vuông góc với \(\left(\beta\right)\). Như vậy \(\Delta\) cắt \(a\) tại \(M\) và cắt \(b\) tại \(N\), đồng thời \(\Delta\) vuông góc với cả \(a\) và \(b\). Do đó \(\Delta\) là đường vuông góc chung của \(a\) và \(b\).
3. Nhận xét
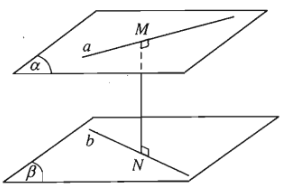
a) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
@2249966@
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh \(a\), \(SA\perp\left(ABCD\right)\) và \(SA=a\). Tính khoảng cách giữa hai đường thẳng chéo nhau \(SC\) và \(BD\).
Giải:
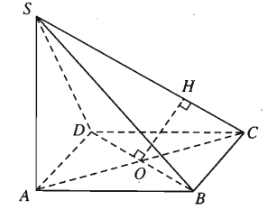
Gọi \(O\) là tâm hình vuông \(ABCD\). Trong mp \(\left(SAC\right)\) vẽ \(OH\perp SC\)
Ta có: \(BD\perp AC\), \(BD\perp SA\) nên \(BD\perp\left(SAC\right)\), suy ra \(BD\perp OH\)
Vậy \(OH\) là đoạn vuông góc chung của \(SC\) và \(BD\) nên \(d\left(SC,BD\right)=OH\)
Chứng minh được \(\Delta SAC\) đồng dạng với \(\Delta OHC\)
Nên \(\dfrac{SA}{SC}=\dfrac{OH}{OC}\left(=\sin C\right)\) \(\Rightarrow OH=\dfrac{SA.OC}{SC}\)
Ta có: \(SA=a\), \(OC=\dfrac{a\sqrt{2}}{2}\), \(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
Từ đó tính được \(OH=\dfrac{a\sqrt{6}}{6}\).
Vậy \(d\left(SC,BD\right)=OH=\dfrac{a\sqrt{6}}{6}\).
@2249787@