Các câu hỏi tương tự
Bài 3. Cho tam giác nhọn ABC nội tiếp (O) , các đường cao AD, BE ,CF cắt nhau tại điểm H .Gọi M là trung điểm của BC , đường tròn tâm I đường kính AH cắt lại (O) tại N (khác A) , AHcắt EF tại K .
a. Chứng minh: E F, nằm trên đường
tròn tâm I và M, H ,N thẳng hàng.
b. Chứng minh: HK/HD=AK/AD
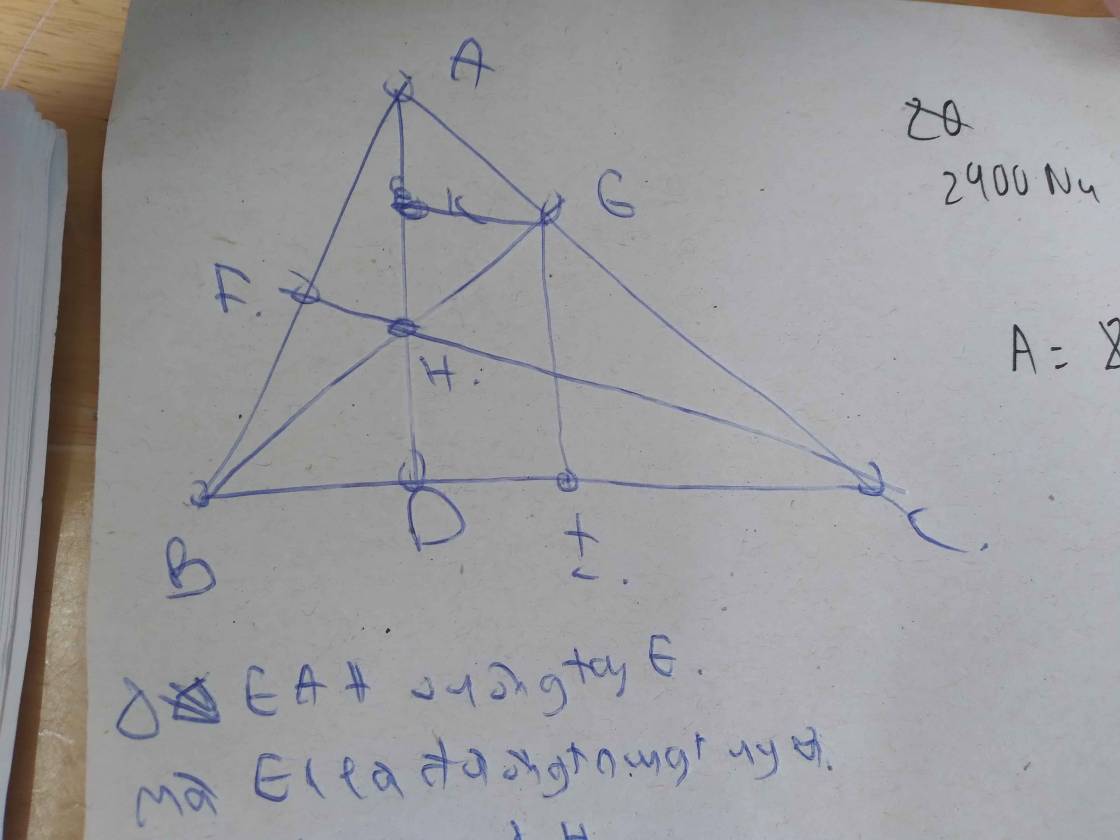
Cho tam giác nhọn ABC có AB AC. Gọi AD, BE, CF là các đường cao và H là trực tâm của tam giác ABC. Vẽ hình bình hành BHCG, đường thẳng G song song với BC cắt AH tại M
a) Chứng minh tứ giác ABGC và tứ giác ABMG nội tiếp được trong đường tròn.
b) Chứng minh tam giác ABD và tam giác AGC đồng dạng.
c) Chứng minh H và M đối xứng với nhau qua BC.
d) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và K là trung điểm của BC, AK cắt OH tại I. Chứng minh rằng I là trọng tâm của tam giác ABC.
Đọc tiếp
Cho tam giác nhọn ABC có AB < AC. Gọi AD, BE, CF là các đường cao và H là trực tâm của tam giác ABC. Vẽ hình bình hành BHCG, đường thẳng G song song với BC cắt AH tại M
a) Chứng minh tứ giác ABGC và tứ giác ABMG nội tiếp được trong đường tròn.
b) Chứng minh tam giác ABD và tam giác AGC đồng dạng.
c) Chứng minh H và M đối xứng với nhau qua BC.
d) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và K là trung điểm của BC, AK cắt OH tại I. Chứng minh rằng I là trọng tâm của tam giác ABC.
Cho tam giác ABC có ba góc nhọn AB<AC 3 đường cao AD, BE, CF cắt nhau ở H
1) chứng minh tứ giác BFEC nội tiếp. Xác định tâm o của đường tròn ngoại tiếp tứ giác này
2) Gọi I là trung điểm của AH. Chứng minh IE là tiếp tuyến của đường tròn o
3) Vẽ CI cắt đường tròn o tại M khác C, EF cắt AD tại K. Chứng minh ba điểm B, K, M thẳng hàng
Cho tam giác ABC có 3 góc nhọn nội tiếp (O). Vẽ các đường cao AD, BE, CF cắt nhau tại H. a/ Chứng mính bốn điểm C, D, ,H,E cùng thuộc một đường tròn tâm I. b/ Chứng minh bốn điểm B, F,E,C cùng thuộc một đường tròn tâm K. c/ Gọi M là trung điểm AH. Chứng minh: góc MEK = 90⁰
cho tam giác ABC có ba góc nhọn nội tiếp (O) (ABCA) các đường cao AD, BE, CF cắt nhau tại H. a, Chứng minh các tứ giác AEHF, ACDF nội tiếp. b, Gọi I là điểm dối xứng của E qua BC, BC cắt AI, EI lần lượt tại L K. Vẽ LN vuuong góc với AC tại N. Chứng minh góc KNL góc DAL. c, Chứng minh ba điểm F,D,I thẳng hàng. d, NK cắt AI tại M. Chứng minh A là tâm đường tròn bàng tiếp trong góc M của tam giác DMN
Đọc tiếp
cho tam giác ABC có ba góc nhọn nội tiếp (O) (AB<CA) các đường cao AD, BE, CF cắt nhau tại H. a, Chứng minh các tứ giác AEHF, ACDF nội tiếp. b, Gọi I là điểm dối xứng của E qua BC, BC cắt AI, EI lần lượt tại L K. Vẽ LN vuuong góc với AC tại N. Chứng minh góc KNL= góc DAL. c, Chứng minh ba điểm F,D,I thẳng hàng. d, NK cắt AI tại M. Chứng minh A là tâm đường tròn bàng tiếp trong góc M của tam giác DMN
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF 2
Đọc tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF =2
cho tam giác nhọn abc có hai đường cao be và cf cắt nhau tại h
a) chứng minh tứ giác aehf nội tiếp đường tròn
b) chứng minh góc fec + góc abc=180
c)gọi d là giao điểm của hai đường thẳng ah và bc. chứng minh h là tâm đường tròn nội tiếp tam giác def
Cho tam giác ABC nhọn (AB AC) vẽ đường tròn tâm O có đường kính BC cắt hai cạnh AB và AC theo thứ tự tại E và F ,gọi H là giao điểm của BE và CF, AH cắt BC tại D. Gọi I là trung điểm AH a. Chứng minh tứ giác AEHF nội tiếp đường tròn tâm I và AD vuông góc BC b. Chứng minh tứ giác OEIF nội tiếp và 5 điểm O, D, E, I, F cùng thuộc một đường tròn C. cho biết BC 6 cm và góc A 60 độ Tính độ dài OI
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) vẽ đường tròn tâm O có đường kính BC cắt hai cạnh AB và AC theo thứ tự tại E và F ,gọi H là giao điểm của BE và CF, AH cắt BC tại D. Gọi I là trung điểm AH
a. Chứng minh tứ giác AEHF nội tiếp đường tròn tâm I và AD vuông góc BC
b. Chứng minh tứ giác OEIF nội tiếp và 5 điểm O, D, E, I, F cùng thuộc một đường tròn
C. cho biết BC = 6 cm và góc A = 60 độ Tính độ dài OI
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H, AH cắt EF tại K. Gọi I là trung điểm AH
1) Gọi M là trung điểm BC, kẻ đường kính AP. Chứng minh M là trung điểm của HP.
2) Chứng minh BH/BA + CH/CA = EF/KA.
3) Gọi S là giao điểm của hai đường thắng OI và MK. Chứng minh AS song song với BC.