Bài 1:
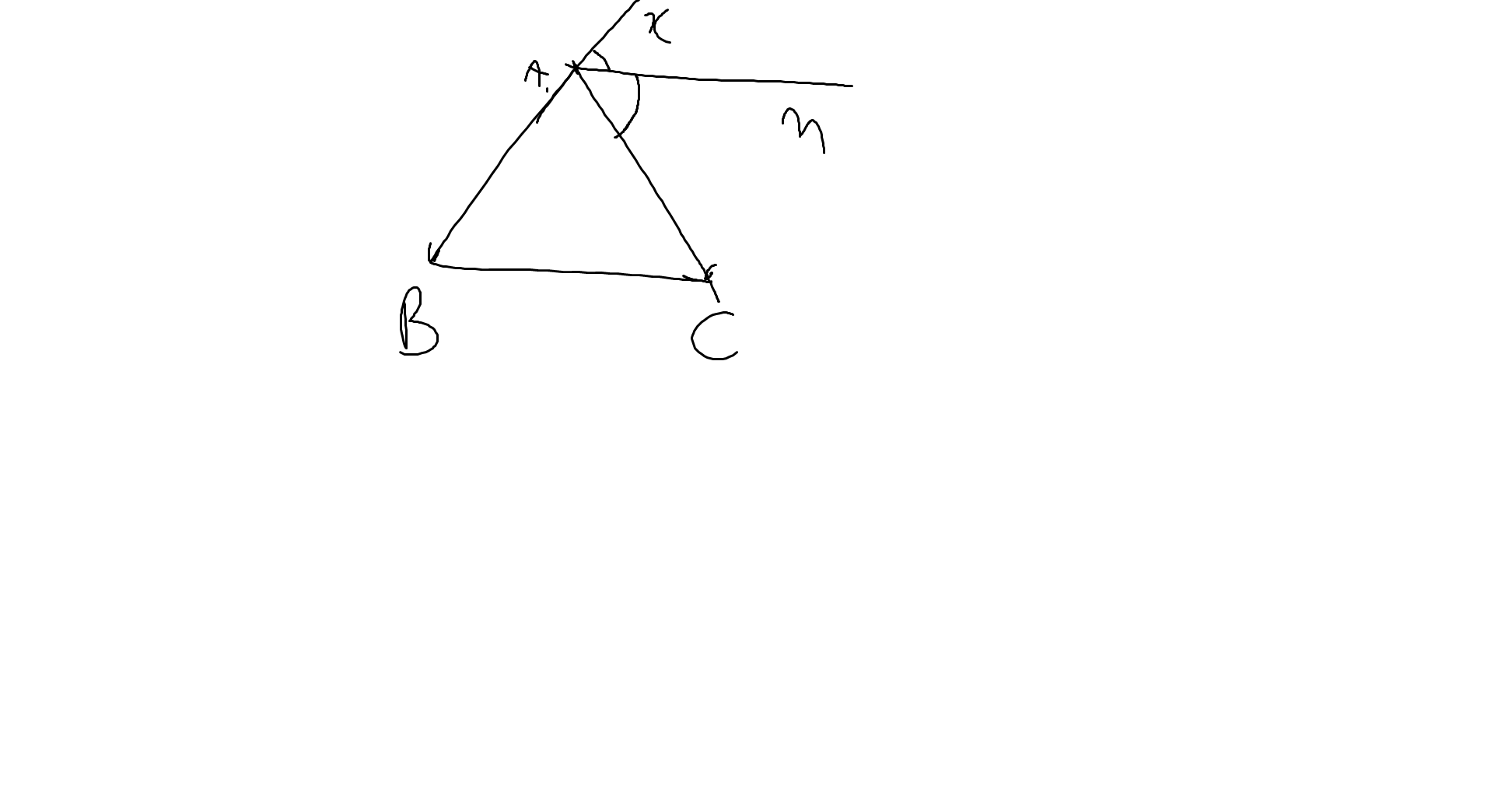
Gọi Ax là tia đối của tia AB
=>\(\widehat{xAC}\) là góc ngoài tại đỉnh A của ΔABC
=>\(\widehat{xAC}=\widehat{ABC}+\widehat{ACB}=50^0+50^0=100^0\)
Am là phân giác của góc xAC
=>\(\widehat{xAm}=\widehat{mAC}=\dfrac{\widehat{xAC}}{2}=\dfrac{100^0}{2}=50^0\)
Ta có: \(\widehat{xAm}=\widehat{ABC}\left(=50^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Am//BC
Bài 2:
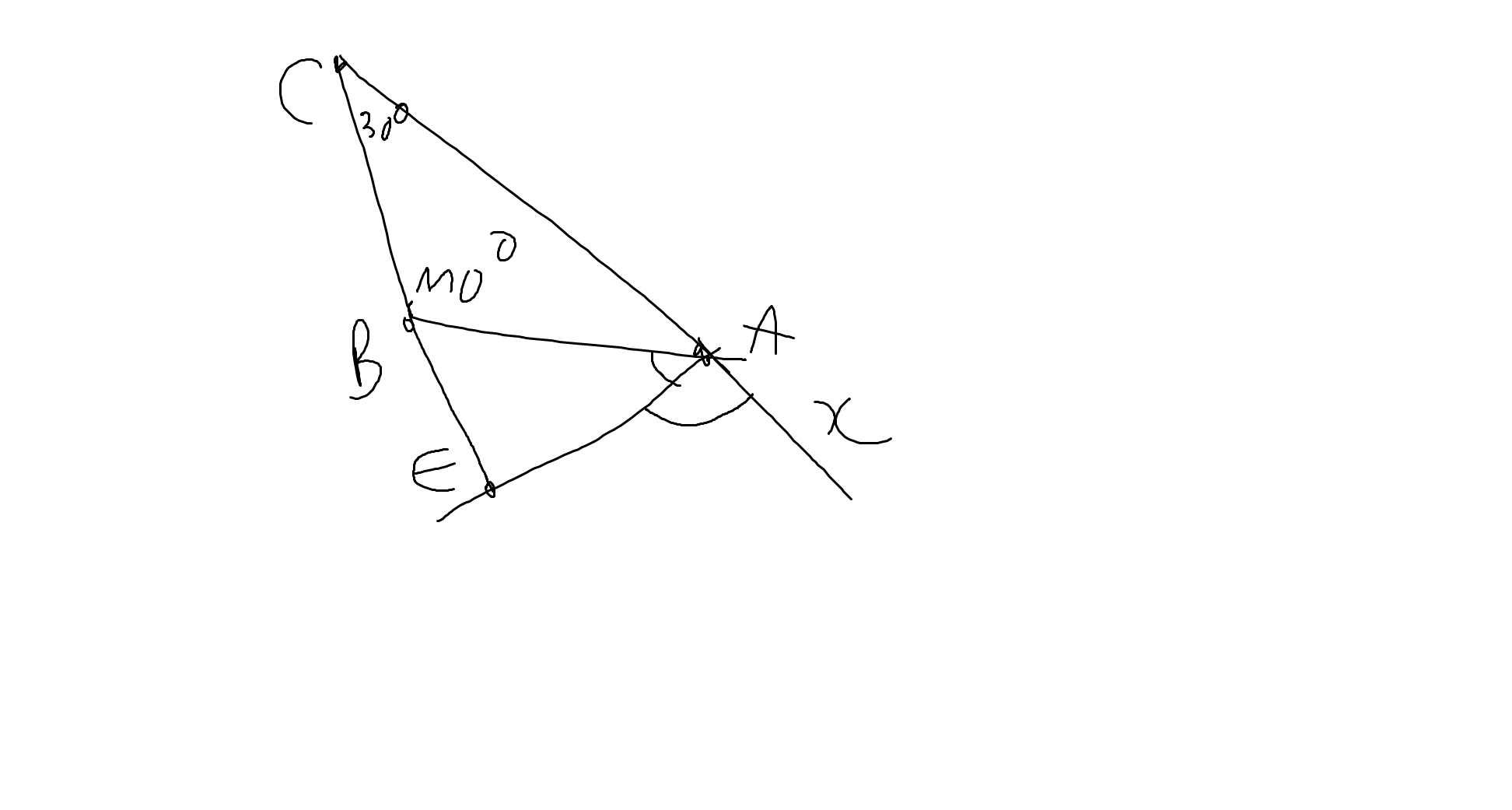
Kẻ Ax là tia đối của tia AC
=>\(\widehat{xAB}\) là góc ngoài tại đỉnh A của ΔABC
=>\(\widehat{xAB}=\widehat{ABC}+\widehat{ACB}=110^0+30^0=140^0\)
AE là phân giác của góc xAB
=>\(\widehat{BAE}=\dfrac{140^0}{2}=70^0\)
Ta có: \(\widehat{ABC}+\widehat{ABE}=180^0\)(hai góc kề bù)
=>\(\widehat{ABE}=180^0-110^0=70^0\)
Xét ΔAEB có \(\widehat{AEB}+\widehat{ABE}+\widehat{BAE}=180^0\)
=>\(\widehat{AEB}=180^0-70^0-70^0=40^0\)
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
