Các câu hỏi tương tự
Cho hình lập phương có cạnh bằng 4. Mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương có bán kính bằng:
A. 2
B. 2 3
C. 2 2
D. 4 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng ABC và AB 2, AC 4,
S
A
3
. Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính A.
R
5
2
B. R5 C.
R
10
3
D.
R
25
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng ABC và AB = 2, AC = 4, S A = 3 . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính
A. R = 5 2
B. R=5
C. R = 10 3
D. R = 25 2
Cho lăng trụ đứng
A
B
C
.
A
B
C
có đáy là tam giác ABC vuông cân tại A,
A
B
a
,
A
A
a
3
. Tính bán kính R của mặt cầu đi qua tất cả các đỉnh của hình lăng trụ theo a. A.
R
a
2...
Đọc tiếp
Cho lăng trụ đứng A B C . A ' B ' C ' có đáy là tam giác ABC vuông cân tại A, A B = a , A A ' = a 3 . Tính bán kính R của mặt cầu đi qua tất cả các đỉnh của hình lăng trụ theo a.
A. R = a 2 2
B. R = a 2
C. R = a 5 2
D. R = 2a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và AB2,AC4,SA
5
. Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là A.
R
5
2
B.
R
5
C.
R
10
3
D.
R
25
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và AB=2,AC=4,SA= 5 . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là
A. R = 5 2
B. R = 5
C. R = 10 3
D. R = 25 2
Cho hình lập phương cạnh a. Diện tích mặt cầu đi qua các đỉnh của hình lập phương là:
A. a 2
B. 2 a 2
C. 3 a 2
D. 4 a 2
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a. A.
a
3
2
B. a C.
2
3
a
D.
a
3
Đọc tiếp
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a.
A. a 3 2
B. a
C. 2 3 a
D. a 3
Cho mặt nón có chiều cao h 6 bán kính đáy r 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương. A.
3
2
2
B.
6
2
-
1...
Đọc tiếp
Cho mặt nón có chiều cao h = 6 bán kính đáy r = 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
A. 3 2 2
B. 6 2 - 1
C. 3 2 + 3
D. 3
Cho hình chóp S.ABC có 4 đỉnh đều nằm trên một mặt cầu, SA a, SB b, SC c và ba cạnh SA, SB, SC đôi một vuông góc. Tính theo a, b, c bán kính mặt cầu đó. A.
1
2
a
2
+
b
2
B.
1
2
b
2
+
c
2...
Đọc tiếp
Cho hình chóp S.ABC có 4 đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính theo a, b, c bán kính mặt cầu đó.
A. 1 2 a 2 + b 2
B. 1 2 b 2 + c 2
C. 1 2 c 2 + a 2
D. 1 2 a 2 + b 2 + c 2
Cho khối đa diện (H) có các đỉnh là tâm các mặt bên của một hình lập phương có cạnh bằng 4. Xét hình nón tròn xoay (N) đi qua tất cả các đỉnh của đa diện (H), đỉnh và tâm đáy của (N) lần lượt là hai đỉnh của đa diện (H) nằm trên hai mặt bên đối lập nhau của hình lập phương (hình vẽ). Thể tích V của khối nón tròn xoay (N) bằng A.
256
π
B.
64
π
C.
64
π
3
D. ...
Đọc tiếp
Cho khối đa diện (H) có các đỉnh là tâm các mặt bên của một hình lập phương có cạnh bằng 4. Xét hình nón tròn xoay (N) đi qua tất cả các đỉnh của đa diện (H), đỉnh và tâm đáy của (N) lần lượt là hai đỉnh của đa diện (H) nằm trên hai mặt bên đối lập nhau của hình lập phương (hình vẽ). Thể tích V của khối nón tròn xoay (N) bằng
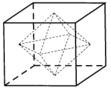
A. 256 π
B. 64 π
C. 64 π 3
D. 16 π 3




