Các câu hỏi tương tự
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là
R
1
,
R
2
,
R
3
. Mệnh đề nào sau đây đúng? A.
R
1
R
3
R
2
B. ...
Đọc tiếp
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là R 1 , R 2 , R 3 . Mệnh đề nào sau đây đúng?
A. R 1 > R 3 > R 2
B. R 1 > R 2 > R 3
C. R 3 > R 1 > R 2
D. R 2 > R 1 > R 3
Cho ba hình cầu tiếp xúc ngoài nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành tam giác có các cạnh bằng 4, 2 và 3. Tích bán kính của ba hình cầu trên là: A. 12 B. 3 C. 6 D. 9
Đọc tiếp
Cho ba hình cầu tiếp xúc ngoài nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành tam giác có các cạnh bằng 4, 2 và 3. Tích bán kính của ba hình cầu trên là:
A. 12
B. 3
C. 6
D. 9
Mặt cầu đi qua tất cả các đỉnh của một hình lập phương cạnh a có bán kính bằng A.
2
a
2
B.
3
a
4
C.
3
a
2
D....
Đọc tiếp
Mặt cầu đi qua tất cả các đỉnh của một hình lập phương cạnh a có bán kính bằng
A. 2 a 2
B. 3 a 4
C. 3 a 2
D. 6 a 4
Cho ba hình cầu tiếp xúc ngoài với nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành một tam giác có các cạnh lần lượt là 4; 2 và 3. Tính tổng bán kính của ba hình cầu trên.
A. 61 12
B. 73 12
C. 14
D. 9
Cho ba hình cầu tiếp xúc ngoài với nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành một tam giác có các cạnh lần lượt là 4; 2 và 3. Tính tổng bán kính của ba hình cầu trên A.
61
12
B.
73
12
C.
14
D.
9
Đọc tiếp
Cho ba hình cầu tiếp xúc ngoài với nhau từng đôi một và cùng tiếp xúc với một mặt phẳng. Các tiếp điểm của các hình cầu trên mặt phẳng lập thành một tam giác có các cạnh lần lượt là 4; 2 và 3. Tính tổng bán kính của ba hình cầu trên
A. 61 12
B. 73 12
C. 14
D. 9
Tính thể tích khối cầu nội tiếp hình lập phương cạnh a (khối cầu tiếp xúc với tất cả các mặt của hình lập phương). A.
π
a
3
2
6
B.
π
a
3
6
C.
π...
Đọc tiếp
Tính thể tích khối cầu nội tiếp hình lập phương cạnh a (khối cầu tiếp xúc với tất cả các mặt của hình lập phương).
A. π a 3 2 6
B. π a 3 6
C. π a 3 8
D. π a 3 6
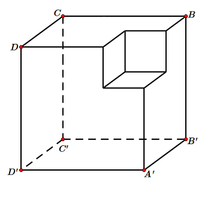
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (ABCD),(BCCB),(DCCD). Tính bán kính của (S). A.
2
+
3
3
B.
3
-
3
C.
2...
Đọc tiếp
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2
Tính bán kính R của mặt cầu ngoại tiếp hình lập phương có cạnh bằng a A.
R
a
3
B.
R
a
2
C.
R
a
3
2
D.
R
a
6
2
Đọc tiếp
Tính bán kính R của mặt cầu ngoại tiếp hình lập phương có cạnh bằng a
A. R = a 3
B. R = a 2
C. R = a 3 2
D. R = a 6 2
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a. A.
a
3
2
B. a C.
2
3
a
D.
a
3
Đọc tiếp
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a.
A. a 3 2
B. a
C. 2 3 a
D. a 3