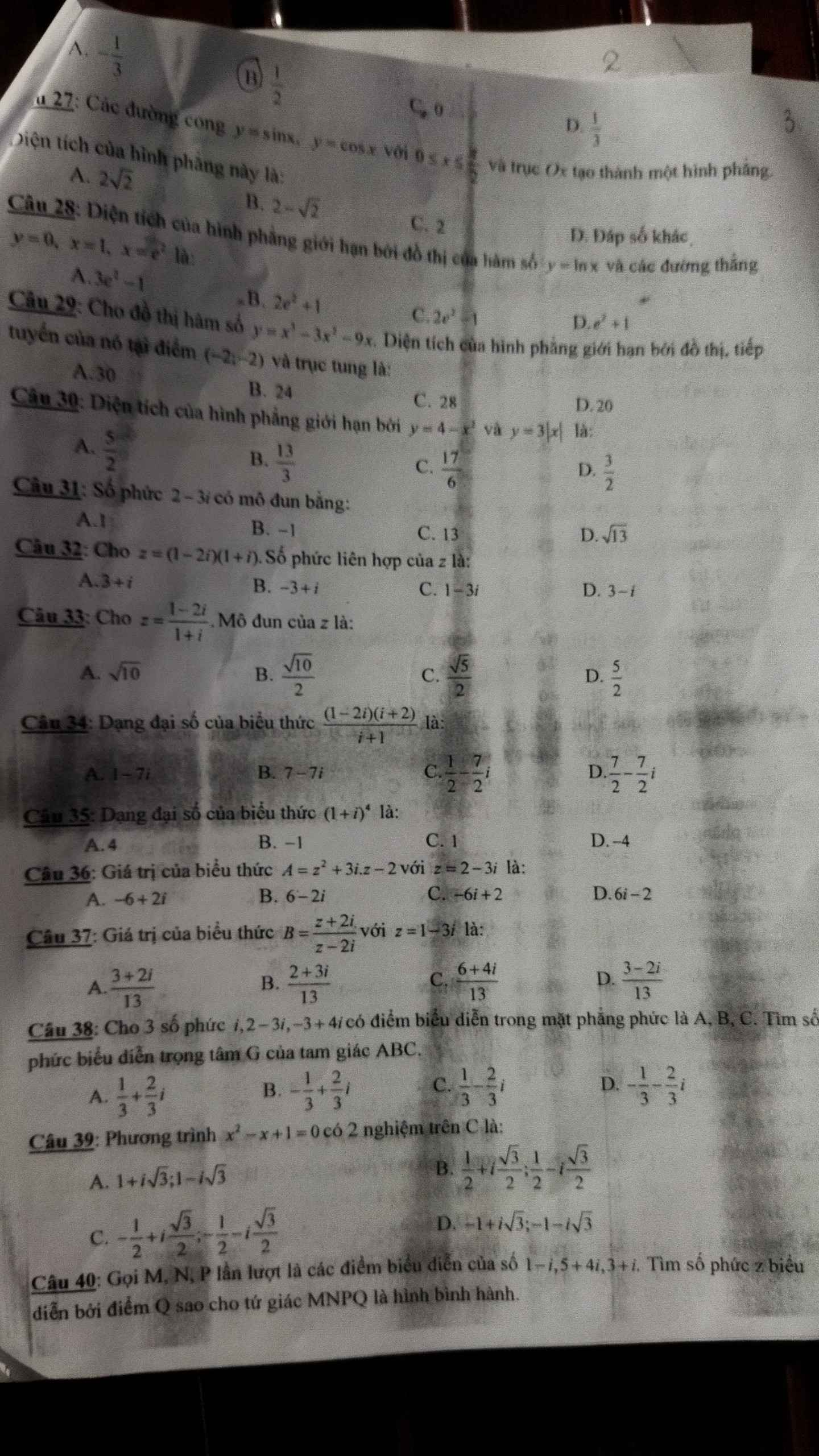Câu 23 ko nhầm thì đã làm rồi
24.
\(\int\limits^4_1\dfrac{1}{x\left(x+1\right)}dx=\int\limits^4_1\left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)dx=\left(lnx-ln\left(x+1\right)\right)|^4_1=ln\left(\dfrac{x}{x+1}\right)|^4_1\)
\(=\ln\left(\dfrac{4}{5}\right)-\ln\left(\dfrac{1}{2}\right)=\ln\left(\dfrac{8}{5}\right)\)
\(0< \ln\left(\dfrac{8}{5}\right)< 1\)
25.
\(\int\limits^2_1\dfrac{x^2}{x+1}dx=\int\limits^2_1\left(x-1+\dfrac{1}{x+1}\right)dx=\left(\dfrac{x^2}{2}-x+ln\left(x+1\right)\right)|^2_1\)
\(=\dfrac{1}{2}+\ln\left(\dfrac{3}{2}\right)\)
Cả 4 đáp án đều sai
26.
\(\int\limits^t_0\dfrac{dx}{x^2-1}=\dfrac{1}{2}\int\limits^t_0\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)dx=\dfrac{1}{2}\left(ln\left|x-1\right|-ln\left|x+1\right|\right)|^t_0\)
\(=\dfrac{1}{2}\ln\left|\dfrac{x-1}{x+1}\right||^t_0=\dfrac{1}{2}\ln\left|\dfrac{t-1}{t+1}\right|=-\dfrac{1}{2}\ln3=\dfrac{1}{2}\ln\left(\dfrac{1}{3}\right)\)
\(\Rightarrow\left|\dfrac{t-1}{t+1}\right|=\dfrac{1}{3}\Rightarrow\left[{}\begin{matrix}t=2\left(loại\right)\\t=\dfrac{1}{2}\end{matrix}\right.\)
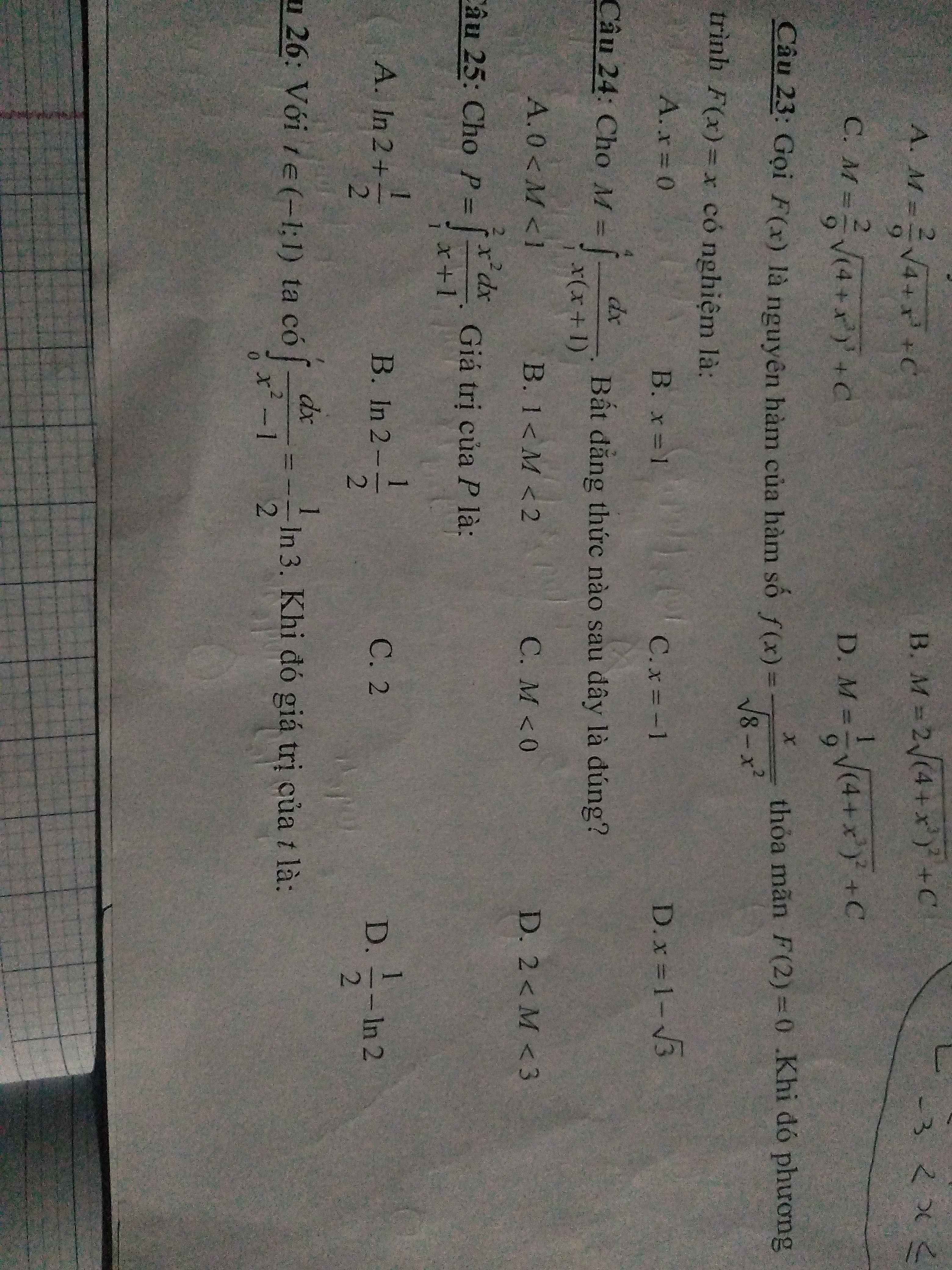
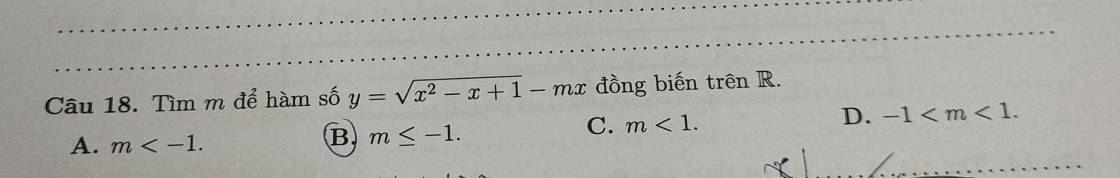
giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
Giúp với
