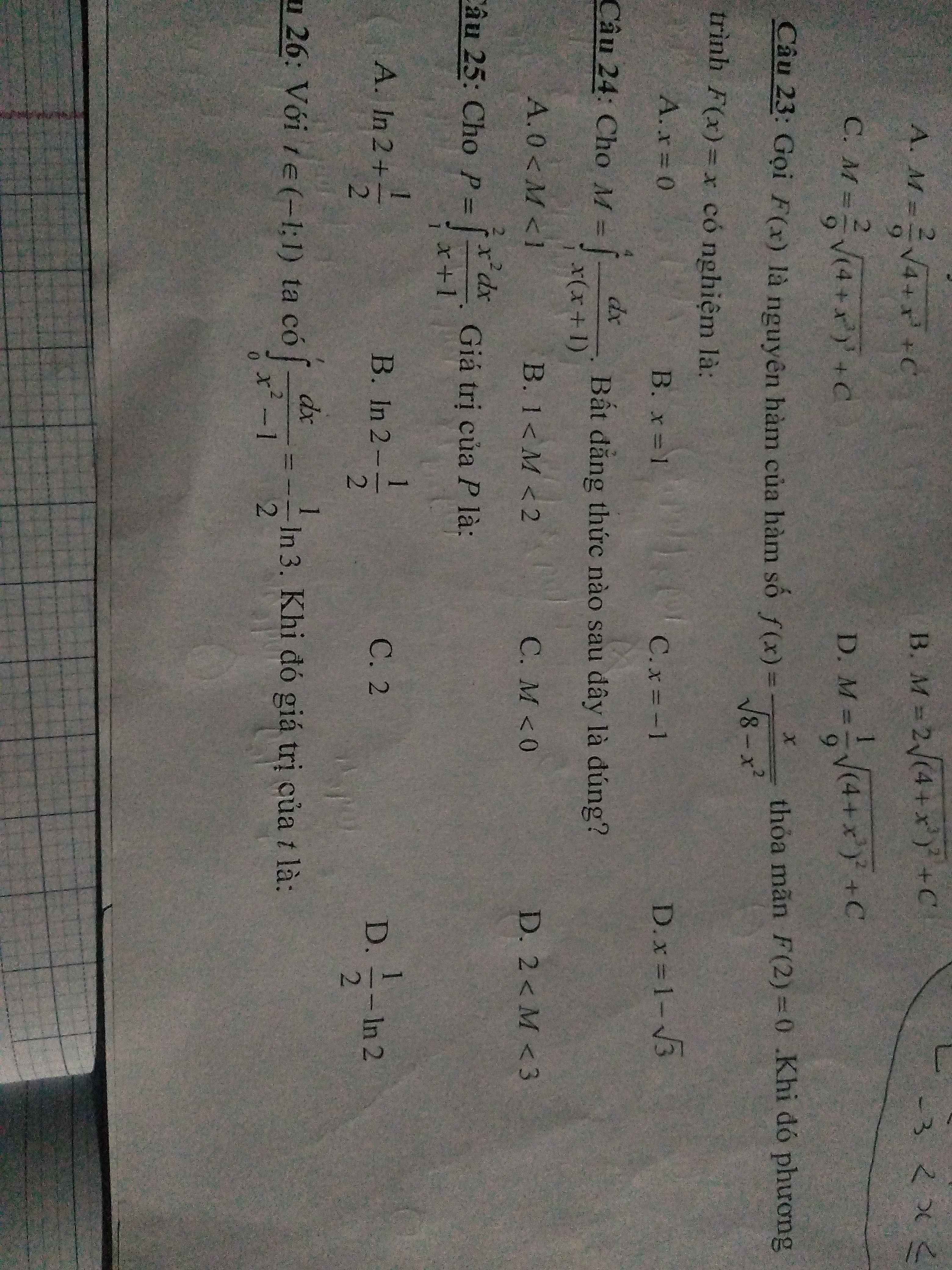16. Không thấy đề
17.
Chắc là: \(\left|log_{0,5}x\right|>6\)?
ĐKXĐ: \(x>0\)
\(\left[{}\begin{matrix}log_{0,5}x>6\\log_{0,5}x< -6\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x< \left(0,5\right)^6\\x>\left(0,5\right)^{-6}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x< \dfrac{1}{64}\\x>64\end{matrix}\right.\)
Kết hợp ĐKXĐ: \(\left[{}\begin{matrix}0< x< \dfrac{1}{64}\\x>64\end{matrix}\right.\) (B)
18.
ĐKXĐ: \(x>\dfrac{5}{3}\)
\(log_{\dfrac{1}{5}}\left(3x-5\right)>log_{\dfrac{1}{5}}\left(x+1\right)\)
\(\Leftrightarrow3x-5< x+1\)
\(\Leftrightarrow x< 3\)
Kết hợp ĐKXĐ \(\Rightarrow\dfrac{5}{3}< x< 3\)
\(\Rightarrow\) Có đúng 1 nghiệm nguyên là \(x=2\)
19.
\(\left(\dfrac{1}{2}\right)^{\dfrac{3x+5}{3+x}}\ge2^{2x+1}\)
\(\Leftrightarrow2^{-\dfrac{3x+5}{3+x}}\ge2^{2x+1}\)
\(\Leftrightarrow-\dfrac{3x+5}{3+x}\ge2x+1\)
\(\Leftrightarrow2x+1+\dfrac{3x+5}{3+x}\le0\)
\(\Leftrightarrow\dfrac{2x^2+10x+8}{3+x}\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-4\\-3< x\le-1\end{matrix}\right.\)
(A)
20.
ĐKXĐ: \(2x^2+5x-3>0\Rightarrow\left[{}\begin{matrix}x>\dfrac{1}{2}\\x< -3\end{matrix}\right.\)
\(log_2\left(2x^2+5x-3\right)>2\)
\(\Leftrightarrow2x^2+5x-3>4\)
\(\Leftrightarrow2x^2+5x-7>0\)
\(\Rightarrow\left[{}\begin{matrix}x>1\\x< -\dfrac{7}{2}\end{matrix}\right.\)
Kết hợp ĐKXĐ ta được: \(\left[{}\begin{matrix}x>1\\x< -\dfrac{7}{2}\end{matrix}\right.\)
(C)
21.
\(I=\int f\left(x\right)dx=\int e^x\left(1-3e^{-2x}\right)dx=\int\left(e^x-3.e^{-x}\right)dx\)
\(=e^x+3e^{-x}+C\)
22.
\(M=\int x^2\sqrt{4+x^3}dx=\dfrac{1}{3}\int\left(4+x^3\right)^{\dfrac{1}{2}}d\left(4+x^3\right)\)
\(=\dfrac{2}{3}.\dfrac{1}{3}\left(4+x^3\right)^{\dfrac{3}{2}}+C=\dfrac{2}{9}\sqrt{\left(4+x^3\right)^3}+C\)
23.
\(F\left(x\right)=\int\dfrac{x}{\sqrt{8-x^2}}dx=-\dfrac{1}{2}\int\left(8-x^2\right)^{-\dfrac{1}{2}}d\left(8-x^2\right)\)
\(=-\left(8-x^2\right)^{\dfrac{1}{2}}+C=-\sqrt{8-x^2}+C\)
\(F\left(2\right)=0\Rightarrow-\sqrt{8-4}+C=0\Rightarrow C=2\)
\(\Rightarrow F\left(x\right)=-\sqrt{8-x^2}+2=x\)
\(\Rightarrow\sqrt{8-x^2}=2-x\left(x\le2\right)\)
\(\Leftrightarrow8-x^2=x^2-4x+4\)
\(\Leftrightarrow2x^2-4x-4=0\Rightarrow\left[{}\begin{matrix}x=1+\sqrt{3}>2\left(loại\right)\\x=1-\sqrt{3}\end{matrix}\right.\)






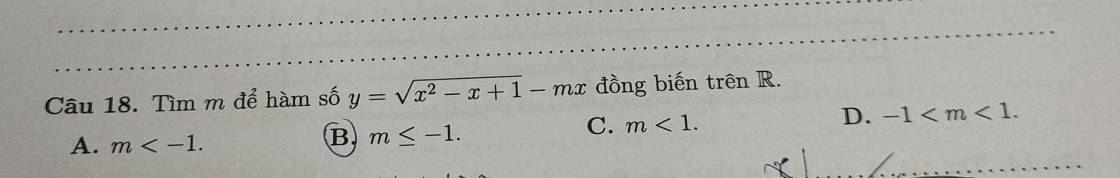

 giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
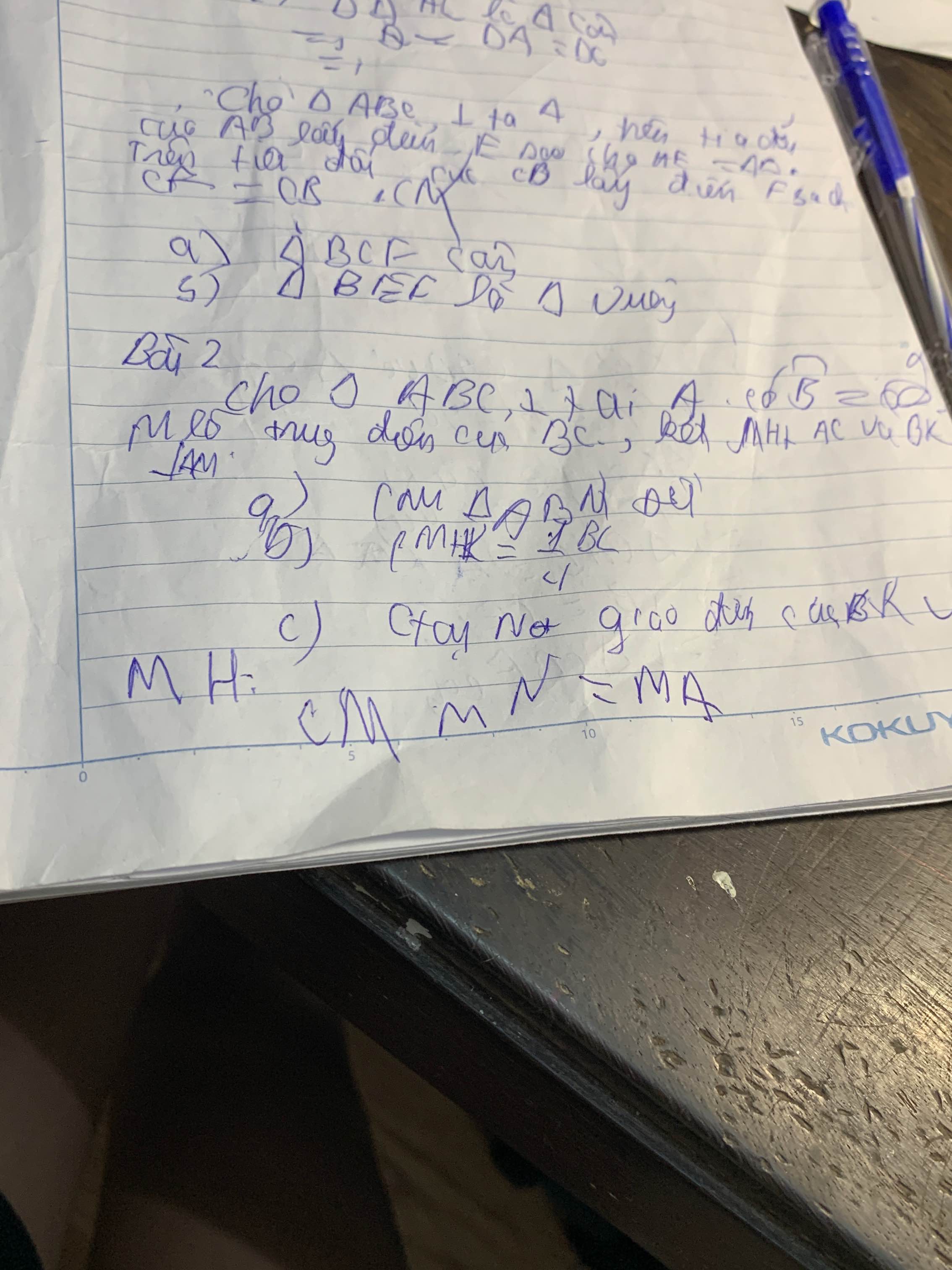

 Giúp với
Giúp với