c: Xét ΔAKB vuông tại K có KM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AK^2\left(1\right)\)
Xét ΔAKC vuông tại K có KN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AK^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN\(\sim\)ΔACB
Đúng 0
Bình luận (0)

 Giúp với
Giúp với



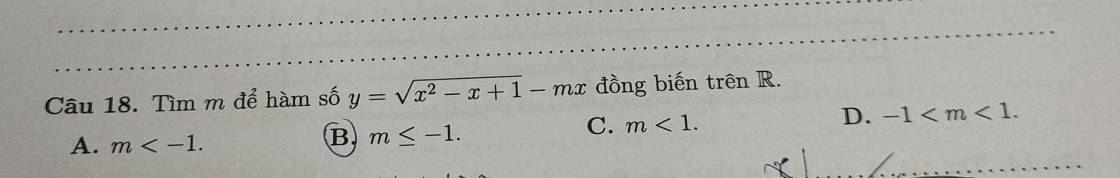








 giúp mk với :(((((((((((
giúp mk với :(((((((((((



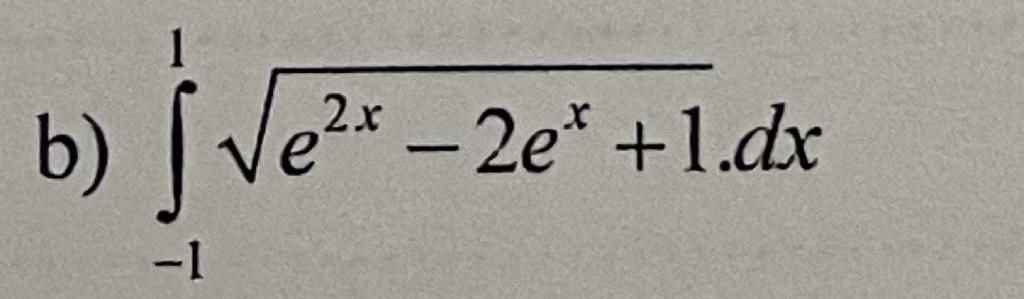 giúp mik với
giúp mik với