Ta xác định : \(D=R\)
\(y=x^4-2x^2+1\Rightarrow'y=4x^3-4x=0\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=+1\end{matrix}\right.\)
\(f\left(0\right)=1,f\left(2\right)=9,f\left(1\right)=0\)
\(\Rightarrow maxy_{\left[0;2\right]}=9\)
Ta xác định : \(D=R\)
\(y=x^4-2x^2+1\Rightarrow'y=4x^3-4x=0\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=+1\end{matrix}\right.\)
\(f\left(0\right)=1,f\left(2\right)=9,f\left(1\right)=0\)
\(\Rightarrow maxy_{\left[0;2\right]}=9\)
Cho hình chóp S.ABC có đáy là tam giác vuông tại C, AB=a 5 , AC=a. Cạnh bên SA=3a và vuông góc vói mặt phẳng (ABC). Thể tích khối chóp S.ABC bằng
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc vói đáy. Gọi M là trung điểm của SC và α là số đo của góc giữa hai đường thẳng AC, BM. Khi đó cos α bằng

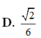
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
Ông A muốn mua một chiếc ô tô trị giá 1 tỉ đồng, nhưng vì chưa đủ tiền nên ông chọn mua bằng hình thức trả góp hàng tháng (số tiền trả góp mỗi tháng là như nhau) với lãi suất 12%/ năm và trả trức 500 triệu đồng. Hỏi mỗi tháng ông phải trả số tiền gần nhất vói số tiền nào dưới đây để sau đúng 2 năm, kể từ ngày mua xe, ông trả hết nợ, biết kỳ trả nợ đầu tiên sau ngày mua ô tô đúng một tháng và chỉ tính lãi hàng tháng trên số dư nợ thực tế của tháng đó?
A. 23.573.000 (đồng).
B. 23.537.000 (đồng).
C. 22.703.000 (đồng).
D. 24.443.000 (đồng).
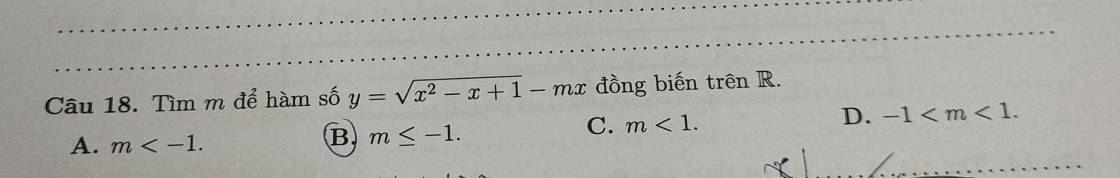 Giúp mình với ghi bước giải ra giúp mình
Giúp mình với ghi bước giải ra giúp mình
 giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
giúp em với ạ, mong mọi người giúp em nhanh nhanh chút ạ
Giúp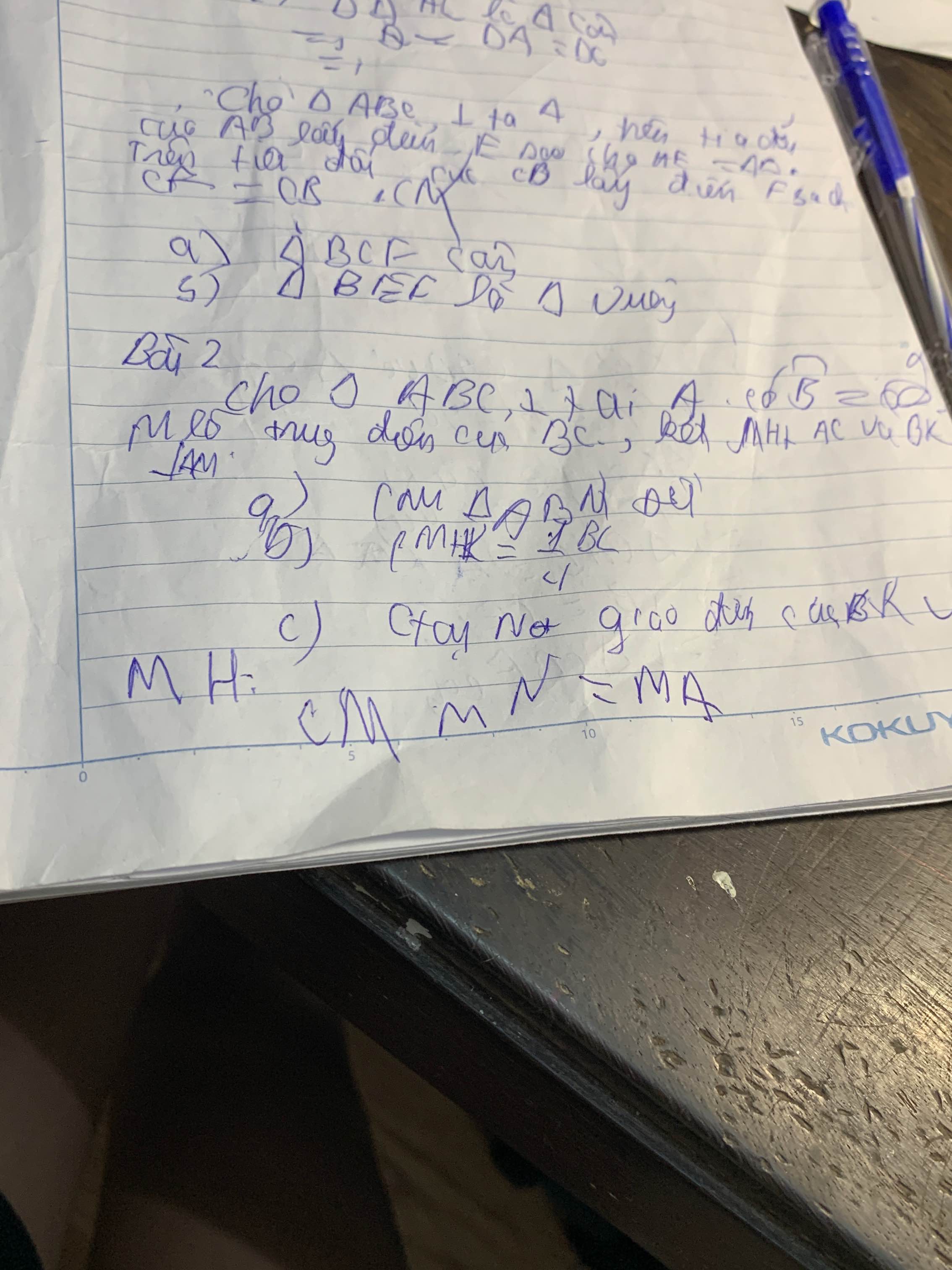
 Giúp với
Giúp với
Giúp ☠️