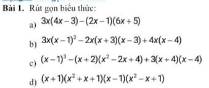a) \(3x\left(4x-3\right)-\left(2x-1\right)\left(6x+5\right)\)
\(=12x^2-9x-\left(12x^2+10x-6x-5\right)\)
\(=12x^2-9x-12x^2-10x+6x+5\)
\(=-13x+5\)
b) \(3x\left(x+1\right)^3-2x\left(x+3\right)\left(x-3\right)+4x\left(x-4\right)\)
\(=3x\left(x^3+3x+3x^2+1\right)-2x\left(x^2-9\right)+4x^2-16x\)
\(=3x^4+9x^2+9x^3+3x-2x^3+18x+4x^2-16x\)
\(=3x^4+7x^3+13x^2+5x\)
c) \(\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)
\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)
\(=3x-57\)
d) \(\left(x+1\right)\left(x^2+x+1\right)\left(x-1\right)\left(x^2-x+1\right)\)
\(=\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)\)
\(=\left(x^3-1\right)\left(x^3+1\right)\)
\(=\left(x^3\right)^2-1\)
\(=x^6-1\)
\(a,3x\left(4x-3\right)-\left(2x-1\right)\left(6x+5\right)\\ =12x^2-9x-12x^2+6x-10x-10\\ =12x^2-12x^2+6x-10x-9x-10\\ =-13x-10\\ b,3x\left(x-1\right)^2-2x\left(x+3\right)\left(x-3\right)+4x\left(x-4\right)\\ =3x\left(x^2-2x+1\right)-2x\left(x^2-9\right)+4x\left(x-4\right)\\ =3x^3-6x^2+3x-2x^2+18x+4x^2-16x\\ =3x^3-2x^2+4x^2-6x^2+3x+18x-16x\\ =3x^3-4x^2+5x\)
a) 3x(4x - 3) - (2x - 1)(6x + 5)
= 12x² - 9x - 12x² - 10x + 6x + 5
= (12x² - 12x²) + (-9x - 10x + 6x) + 5
= -13x + 5
b) 3x(x - 1)² - 2x(x + 3)(x - 3) + 4x(x - 4)
= 3x(x² - 2x + 1) - 2x(x² - 9) + 4x² - 16x
= 3x³ - 6x² + 3x - 2x³ + 18x + 4x² - 16x
= (3x³ - 2x³) + (-6x² + 4x²) + (3x + 18x - 6x)
= x³ - 2x² + 15x
c) (x - 1)³ - (x + 2)(x² - 2x + 4) + 3(x + 4)(x - 4)
= x³ - 3x² + 3x - 1 - x³ - 8 + 3x² + 48x
= (x³ - x³) + (-3x² + 3x²) + (3x + 48x) + (-1 - 8)
= 51x - 9
d) (x + 1)(x² + x + 1)(x - 1)(x² - x + 1)
= [(x + 1)(x² - x + 1)][(x - 1)(x² + x + 1)]
= (x³ + 1³)(x³ - 1³)
= x⁶ - 1⁶
= x⁶ - 1