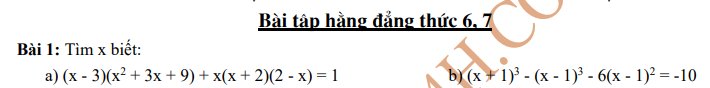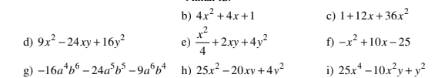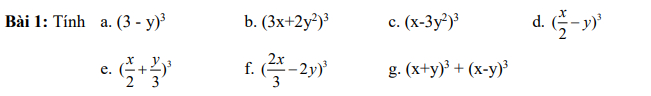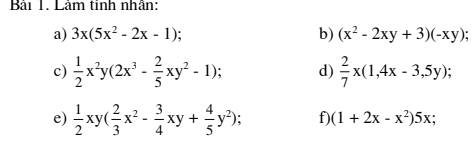a) \(x^3+6x^2+12x+8\)
\(=x^3+3\cdot x^2\cdot2+3\cdot2^2\cdot x+2^3\)
\(=\left(x+2\right)^3\)
b) \(x^3-3x^2+3x-1\)
\(=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3\)
\(=\left(x-1\right)^3\)
c) \(1-9x+27x^2-27x^3\)
\(=1^3-3\cdot3x\cdot1^2+3\cdot\left(3x\right)^2\cdot1-\left(3x\right)^3\)
\(=\left(1-3x\right)^3\)
d) \(x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}\)
\(=x^3\cdot3\cdot\dfrac{1}{2}\cdot x^2+3\cdot\left(\dfrac{1}{2}\right)^2\cdot x+\left(\dfrac{1}{2}\right)^3\)
\(=\left(x+\dfrac{1}{2}\right)^3\)
e) \(27x^3-54x^2y+36xy^2-8y^3\)
\(=\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot y+3\cdot x\cdot\left(2y\right)^2-\left(2y\right)^3\)
\(=\left(3x-2y\right)^3\)