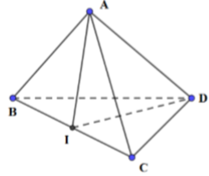
Gọi I là trung điểm của BC
Ta có:
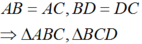
là hai tam giác cân lần lượt tại đỉnh A và D.
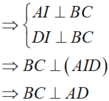
Chọn: C

Gọi I là trung điểm của BC
Ta có:
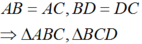
là hai tam giác cân lần lượt tại đỉnh A và D.
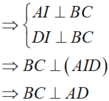
Chọn: C
Cho ba đường thẳng song song a,b,c. Gọi d là đường thẳng cắt a nhưng không cắt b và c. Xét đường thẳng D cắt d và song song với b. Khẳng định nào sau đây đúng?
A. ∆ ⊂ m p a , d
B. ∆ ⊂ m p a , b
C. ∆ ⊂ m p a , c
D. ∆ ⊂ m p b , c
Cho hàm số y = ax 3 + bx 2 + cx + d (a,b,c,d là các hằng số,a≠0) có đồ thị như sau:
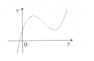
Khẳng định nào sau đây là khẳng định đúng?
A. abcd > 0.
B a–b+c+d < 0.
C. a–b+c+d > 0.
D. abcd = 0.
Cho hai tập hợp A={a,b,c,d};B={c,d,e}. Chọn khẳng định sai trong các khẳng định sau:
A. N A ∩ B = 2
B. N(A)=4.
C. N(B)=3.
D. N A ∪ B = 7
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho A={a;b;c} và B={a;c;d;e}.Hãy chọn khẳng định đúng
A. A ∩ B = a ; b ; c ; d ; e
B. A ∩ B = a
C. A ∩ B = a ; c
D. A ∩ B = d ; e
Cho hàm số y = a x 3 + b x 2 + c x + d , a , b , c , d ∈ ℝ có đồ thị như dưới đây. Tìm khẳng định đúng trong các khẳng định sau?
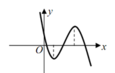
A. a < 0, b < 0, c < 0, d > 0, b 2 > 3 a c
B. a < 0, b < 0, c > 0, d > 0, b 2 > 3 a c
C. a < 0, b > 0, c < 0, d > 0, b 2 > 3 a c
D. a < 0, b > 0, c > 0, d > 0, b 2 > 3 a c
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt A B → = b → ; A C → = c → ; A D → = d → . Khẳng định nào sau đây đúng?
A. M P → = 1 2 d → + c → - b →
B. M P → = 1 2 c → + d → + b →
C. M P → = 1 2 c → + b → - d →
D. M P → = 1 2 d → + b → - c →
Trong không gian với tọa độ Oxyz, cho tứ diện ABCD với A(0;0;3), B(0;0;-1), C(1;0;-1), D(0;1;-1). Mệnh đề nào sau đây là sai?
A. AB ⊥ BD
B. AB ⊥ BC
C. AB ⊥ AC
D. AB ⊥ CD
Đồ thị hàm số y = ax3 + bx2 + cx + d (a, b, c, d là các hằng số thực và a ≠ 0) như hình vẽ.
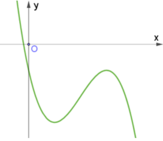
Khẳng định nào đúng
A. b > 0, c > 0
B. b < 0, c < 0
C. b < 0, c > 0
D. b > 0, c < 0
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD với A(1;2;1), B(–2;1;3), C(2;–1;1), D(0;3;1). Viết phương trình mặt phẳng (P) chứa hai điểm A, B sao cho C, D nằm về hai phía khác nhau của (P) đồng thời C, D cách đều (P)
A. (P) : 2x + 3z – 5 = 0
B. P) : 4x + 2y + 7z – 15 = 0
C. (P) : 3y + z – 1 = 0
D. (P) : x – y + z – 5 = 0