Các câu hỏi tương tự
Cho hàm số
y
ax
3
+
bx
2
+
cx
+
d
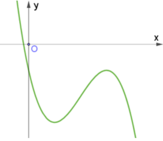
(a,b,c,d là các hằng số,a≠0) có đồ thị như sau:Khẳng định nào sau đây là khẳng định đúng? A. abcd 0. B a–b+c+d 0. C. a–b+c+d 0. D. abcd 0.
Đọc tiếp
Cho hàm số y = ax 3 + bx 2 + cx + d (a,b,c,d là các hằng số,a≠0) có đồ thị như sau:
Khẳng định nào sau đây là khẳng định đúng?
A. abcd > 0.
B a–b+c+d < 0.
C. a–b+c+d > 0.
D. abcd = 0.
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số
y
ax
3
+
bx
2
+
cx
+
d
,
a
≠
0
có đồ thị như hình vẽ sau. Khẳng định nào sau đây là đúng? A.
a
0
;
b
2
−
3
ac
0
B. ...
Đọc tiếp
Cho hàm số y = ax 3 + bx 2 + cx + d , a ≠ 0 có đồ thị như hình vẽ sau. Khẳng định nào sau đây là đúng?
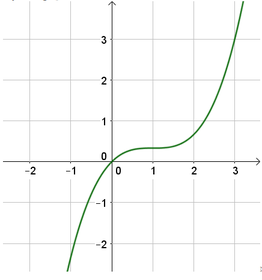
A. a > 0 ; b 2 − 3 ac = 0
B. a < 0 ; b 2 − 3 ac ≤ 0
C. a < 0 ; b 2 − 3 ac = 0
D. a > 0 ; b 2 − 3 ac ≤ 0
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
(
a
≠
0
)
có đồ thị như hình vẽ. Khẳng định nào sau đây đúng? A.
a
0,
d
0
;
b
0,
c
...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d ( a ≠ 0 ) có đồ thị
như hình vẽ. Khẳng định nào sau đây đúng?
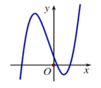
A. a > 0, d > 0 ; b < 0, c < 0.
B. a < 0, b < 0, c < 0 ; d > 0
C. a > 0, c > 0, d > 0 ; b < 0.
D. a > 0, b > 0, d > 0 ; c < 0
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
a
≠
0
có đồ thị như hình vẽ. Chọn khẳng định đúng? A.
a
0,
d
0.
B.
a
0,
b
0,
...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d a ≠ 0 có đồ thị như hình vẽ. Chọn khẳng định đúng?
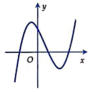
A. a > 0, d > 0.
B. a > 0, b < 0, c > 0.
C. a > 0, b > 0, c > 0, d > 0.
D. a > 0, c < 0, d > 0.
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
,
a
≠
0...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d a , b , c , d ∈ ℝ , a ≠ 0 có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ' x cho bởi hình vẽ
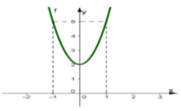
Giá trị f 3 - 2 f 1 là
A. 6
B. 5
C. 28
D. 26
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
(với a,b,c,d ϵ ℝ và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số
g
x
f
-
2
x
2
+
4...
Đọc tiếp
Cho hàm số f x = a x 3 + b x 2 + c x + d (với a,b,c,d ϵ ℝ và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số g x = f - 2 x 2 + 4 x là
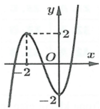
A. 2.
B. 3.
C. 4.
D. 5.
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
a
,
b
,
c
∈
ℝ
,
a
≠
0
)
có đồ thị (C). Biết đồ thị (C)đi qua A(1;4) và đồ thị hàm số
y
f...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c ∈ ℝ , a ≠ 0 ) có đồ thị (C). Biết đồ thị (C)đi qua A(1;4) và đồ thị hàm số y ' = f x cho bởi hình vẽ.
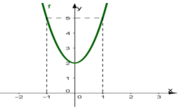
Giá trị f 3 − 2 f 1 là
A. 30
B. 27
C. 25
D. 26
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số
y
f
’
(
x
)
cho bởi hình vẽ. Giá trị
f
(
3
)
-
2...
Đọc tiếp
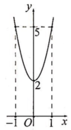
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a,b,cÎR, a≠0) có đồ thị (C). Biết đồ thị (C) đi qua A(1;4) và đồ thị hàm số y = f ’ ( x ) cho bởi hình vẽ. Giá trị f ( 3 ) - 2 f ( 1 ) là
A. 30
B. 24
C. 26
D. 27