Đáp án D
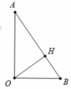
Ta có O A . sin O A H ^ = O H = a ⇒ O A = 2 a
Lại có O B = O A tan A ^ = 2 a 3 suy ra thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA là V = 1 3 πOB 2 . OA = 8 9 πa 3
Đáp án D

Ta có O A . sin O A H ^ = O H = a ⇒ O A = 2 a
Lại có O B = O A tan A ^ = 2 a 3 suy ra thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA là V = 1 3 πOB 2 . OA = 8 9 πa 3
Cho tam giác AOB vuông tại O, có O A B ^ = 30 0 và AB = a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = π a 2 2 .
B. S x q = π a 2 .
C. S x q = π a 2 4 .
D. S x q = 2 π a 2 .
Trong không gian cho tam giác OIM vuông tại I, I O M ^ = 30 ∘ , IM = a. Khi quay tam giác OIM quanh cạnh OI thì tạo thành một hình nón tròn xoay. Tính thể tích khối nón tròn xoay được tạo thành.
A. π a 3 3
B. π a 3 3
C. 2 π a 3 3
D. 2 π a 3 3
Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x = π , y = 0 và y = − sin x . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
A. V = π ∫ 0 π sin x d x .
B. V = π ∫ 0 π sin 2 x d x .
C. V = π ∫ 0 π − sin x d x .
D. V = ∫ 0 π sin 2 x d x .
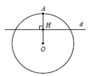
Cho đường tròn (C) tâm O, bán kính R = O A = 3. Đường thẳng d vuông góc với OA tại H. Gọi V 1 , V 2 lần lượt là thể tích của hai khối tròn xoay H 1 , H 2 khi quay hình tròn (C) quanh trục OA với H 1 là khối tròn xoay chứa điểm A. Tính độ dài AH, biết V 2 = 2 V 1
A. 2,32
B. 2,08
C. 1,83
D. 1,56
Cho hình phẳng (D) giới hạn bởi các đường: y = x - π ; y = sinx ; x = 0 . Gọi V là thể tích khối tròn xoay tạo thành do (D) quay quanh trục hoành và V = p π 4 p ∈ ℚ . Giá trị của 24p bằng:
A. 8
B. 4
C. 24
D. 12
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V 1 . Tam giác ABC quay xung
quanh trục d được khối tròn xoay có thể tích là V 2 . Tính tỉ số V 1 V 2 .
A. 2 3
B. 1 3
C. 3
D. 3 2
Cho tam giác OAB vuông tại O, OA=OB=4. Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng
A. 256 81 π
B. 81 256 π
C. 128 81 π
D. 8 3 π
Cho tam giác OAB vuông tại O, O A = O B = 4 Lấy một điểm M thuộc cạnh AB và gọi H là hình chiếu của M trên OA. Thể tích của khối tròn xoay được tạo thành khi quay tam giác OMH quanh OA có thể tích lớn nhất bằng
A. 256 π 81
B. 81 π 256
C. 128 π 81
D. 8 π 3
Cho tam giác OAB vuông tại O, OA = 3cm, OB = 4cm. Quay tam giác OAB quanh cạnh AB. Thể tích khối tròn xoay được tạo thành gần nhất giá trị nào?
A. 28 c m 3
B. 26 c m 3
C. 32 c m 3
D. 30 c m 3