Chọn C.
Ta có: z 2 = ( a + bi ) 2 = a 2 - b 2 + 2 abi . Để z 2 là số thuần ảo thì a 2 - b 2 = 0 ⇔ a = ± b .
Chọn C.
Ta có: z 2 = ( a + bi ) 2 = a 2 - b 2 + 2 abi . Để z 2 là số thuần ảo thì a 2 - b 2 = 0 ⇔ a = ± b .
Cho hai số phức z = - 2 + 5 i , z ’ = a + b i a , b ∈ R . Xác định a,b để z + z’ là một số thuần ảo
A. a = 2 , b = - 5
B. a ≠ 2 , b = - 5
C. a ≠ 2 , b ≠ - 5
D. a = 2 , b ≠ - 5
Cho số phức z = a+bi a , b ∈ R thoả mãn z - 2 i z - 2 là số thuần ảo. Khi số phức z có môđun lớn nhất. Tính giá trị biểu thức P=a+b
A. P = 0
B. P = 4
C. P = 2 2 + 1
D. P = 1 + 3 2
Cho số phức z = a + b i ( a , b ∈ R ) . Xét các mệnh đề sau :
(1) z là số thực khi và chỉ khi a ≠ 0 , b = 0
(2) z là số thuần ảo khi và chỉ khi a = 0 , b ≠ 0
(3) z vừa là số thực vừa là số thuần ảo khi và chỉ khi a = 0, b = 0
Số mệnh đề đúng là ?
A. 2
B. 0
C. 3
D. 1
Cho hai số phức z = a + bi ; a , b ∈ ℝ . Có điểm biểu diễn của số phức z nằm trong dải − 2 ; 2 (hình 1) điều kiện của a và b là: a ≥ 2 b ≥ 2 a ≤ − 2 b ≤ − 2 − 2 < a < 2 , b ∈ ℝ a , b ∈ − 2 ; 2
A. a ≥ 2 b ≥ 2
B. a ≤ − 2 b ≤ − 2
C. − 2 < a < 2 , b ∈ ℝ
D. a , b ∈ − 2 ; 2
Số phức z=a+bi(a,b ∈ R) là số thuần ảo khi và chỉ khi
A.a=0,b#0
B.a#0,b=0
C. a = 0
D. b = 0
Cho số phức z = a + b i , a , b ∈ R . Tìm điều kiện của a và b để điểm biểu diễn của z thuộc dải giới hạn bởi đường thẳng x = - 2 và x = 2 như hình vẽ bên
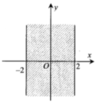
A. a ≥ 2 b ≥ 2
B. a ≤ 2 b ≤ - 2
C. a ≤ 2 b ≥ - 2
D. - 2 ≤ a ≤ 2 b ∈ R
Cho hai số phức:
z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ ) .
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' − a ' b
D. a a ' − b b '
Số phức z=a+bi ( a , b ∈ R ) là một số thuần ảo khi và chỉ khi
A. a = 0 b ≠ 0
B. a = 0
C. a ≠ 0 b = 0
D. b = 0
Cho số phức z = a + b i với a , b ∈ ℝ . Nếu z là số thuần ảo thì đâu là khẳng định đúng?
A. a = 0
B. a = 0 và b ≠ 0
C. b = 0
D. b = 0 và a ≠ 0