Question

Cho hình chóp S.ABC có độ dài các cạnh: S A = B C = x ,    S B = A C = y ,    S C = A B = z thỏa mãn x 2 + y 2 + z 2 = 12 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.

A. 2 3

B.  8 3

C.  2 2 3

Answer 1

Đáp án C

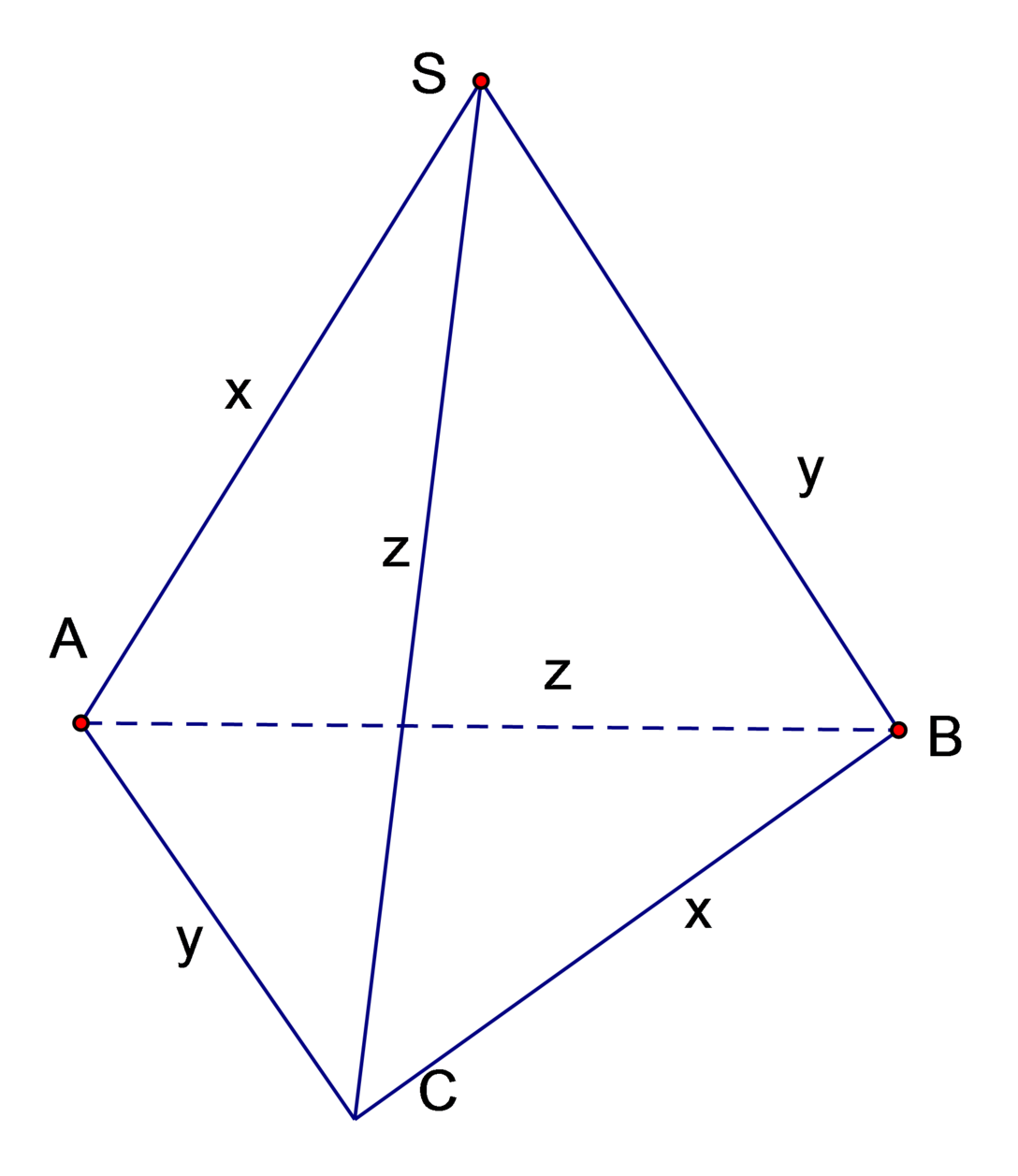
Áp dụng công thức tính thể tích tứ diện có hai cặp cạnh đối bằng nhau:

V S A B C = 1 6 2 x 2 + y 2 − z 2 y 2 + z 2 − x 2 z 2 + x 2 − y 2 ≤ 1 6 2 x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + z 2 + x 2 − y 2 3 3 = 1 6 2 x 2 + y 2 + z 2 3 3 = 1 6 2 12 3 3 = 1 6 2 .8 = 2 2 3

Như vậy V S A B C  lớn nhất bằng 2 2 3  khi: x=y=z=2