Bài 6. Cho tam giác ABC có AB = AC, AD ⊥ BC tại D.
a) Chứng minh BD = CD.
b) Vẽ DH ⊥ AB tại H và DK ⊥ AC tại K. Chứng minh DH = DK.
c) Chứng minh HK // BC.
Bài 6. Cho tam giác ABC có AB = AC, AD ⊥ BC tại D.
a) Chứng minh BD = CD.
b) Vẽ DH ⊥ AB tại H và DK ⊥ AC tại K. Chứng minh DH = DK.
c) Chứng minh HK // BC.
a) \(\Delta\) ABC có
AB = AC (gt)
=> \(\Delta\) ABC cân tại A.
AD là đường cao của tam giác ABC (gt)
=> AD cũng là đường trung tuyến của tam giác ABC (tính chất tam giác cân).
=> BD = CD (đpcm).
b)Xét tam giác vuông ADH và tam giác vuông ADK:
AD là cạnh chung.
\(\widehat{HAD}=\widehat{KAD}\) (do AD là phân giác của \(\widehat{BAC}\)).
=> ΔADH = ΔADK (cạnh huyền - góc nhọn).
=> DH = DK (hai cạnh tương ứng) (đpcm).
c)\(\Delta\) ABC có AB = AC (gt) => Tam giác ABC cân tại A.
=> \(\widehat{ABC}=\widehat{ACB}\)(tính chất tam giác cân).
\(\Delta\) ADH có DH ⊥ AB => \(\widehat{AHD}\)= 90°.
\(\Delta\) ADK có DK ⊥ AC => \(\widehat{AKD}\) = 90°.
Xét \(\Delta\) AHK có:
AH = AK (do ΔADH = ΔADK).
=> Tam giác AHK cân tại A.
=> \(\widehat{AHK}=\widehat{AKH}\)
Mà \(\widehat{AHK}+\widehat{BHD}\) = 180° (kề bù).
\(\widehat{AKH}+\widehat{CKD}\) = 180° (kề bù).
Mặt khác, \(\widehat{BHD}=\widehat{CKD}\) (cùng phụ với \(\widehat{BAD}\)).
=> \(\widehat{AHK}=\widehat{AKH}=\widehat{ABC}=\widehat{ACB}\)
Xét tứ giác BCHK có:
\(\widehat{AHK}=\widehat{ABC}\) (cmt)
Mà hai góc này ở vị trí đồng vị.
=> HK // BC (đpcm).
Gấp ạaa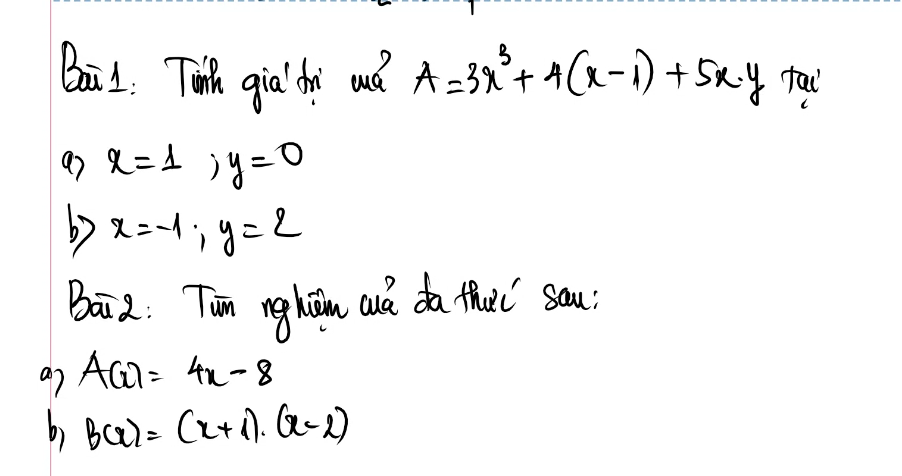
Bài 1: Tính giá trị của \( A = 3x^3 + 4(x-1) + 5x \cdot y \) tại
a) \( x = 1 \), \( y = 0 \)
b) \( x = -1 \), \( y = 2 \)
Bài 2: Tìm nghiệm của đa thức sau:
a) \( A(x) = 4x - 8 \)
b) \( B(x) = (x + 1)(x - 2) \)
Bài 1:
a) Thay `x = 1; y = 0` vào A được:
`A = 3 . 1^3 + 4 . (1-1) +5 .1.0`
`= 3 + 4.0 + 0`
`= 3+0`
`= 3`
b) Thay `x = -1; y = 2` vào A được:
`A = 3 . (-1)^3 + 4 . (-1-1) +5 .(-1).2`
`= -3 + 4 . (-2) + 10 . (-1) `
`= -3 - 8 - 10`
`= -21`
Bài 2:
A(x) có nghiệm <=> `4x - 8 = 0`
`<=> x = 8 : 4`
`<=> x = 2`
Vậy ...
B(x) có nghiệm `<=> (x+1)(x-2) = 0`
`<=> x + 1 = 0` hoặc `x - 2 = 0`
`<=> x = -1` hoặc `x = 2`
Vậy ...
bài 1: a. thay x = 1; y = 0 vào A ta được:
\(A=3\cdot1^3+4\cdot\left(1-1\right)+5\cdot1\cdot0\\ =3\cdot1^3+0+0=3\)
b. thay x = -1; y = 2 vào A ta được:
\(A=3\cdot\left(-1\right)^3+4\cdot\left(-1-1\right)+5\cdot\left(-1\right)\cdot2\\ =-3+\left(-8\right)+\left(-10\right)=-21\)
bài 2: a. 4x - 8 = 0
=> 4x = 8 => x = 2
b. (x - 1)(x - 2) = 0
\(=>\left[{}\begin{matrix}x+1=0=>x=-1\\x-2=0=>x=2\end{matrix}\right.\)
Bài 1: Tính giá trị của \( A = 3x^3 + 4(x-1) + 5x \cdot y \) tại
a) \( x = 1 \); \( y = 0 \)
b) \( x = -1 \); \( y = 2 \)
Bài 2: Tìm nghiệm của đa thức sau:
a) \( A(x) = 4x - 8 \)
b) \( B(x) = (x + 1)(x - 2) \)
Bài 1:
a) Thay `x = 1; y = 0` vào A được:
`A = 3 . 1^3 + 4 . (1-1) +5 .1.0`
`= 3 + 4.0 + 0`
`= 3+0`
`= 3`
b) Thay `x = -1; y = 2` vào A được:
`A = 3 . (-1)^3 + 4 . (-1-1) +5 .(-1).2`
`= -3 + 4 . (-2) + 10 . (-1) `
`= -3 - 8 - 10`
`= -21`
Bài 2:
A(x) có nghiệm <=> `4x - 8 = 0`
`<=> x = 8 : 4`
`<=> x = 2`
Vậy ...
B(x) có nghiệm `<=> (x+1)(x-2) = 0`
`<=> x + 1 = 0` hoặc `x - 2 = 0`
`<=> x = -1` hoặc `x = 2`
Vậy ...
bài 1: a. thay x = 1; y = 0 vào A ta được:
\(A=3\cdot1^3+4\cdot\left(1-1\right)+5\cdot1\cdot0\\ =3\cdot1^3+0+0=3\)
b. thay x = -1; y = 2 vào A ta được:
\(A=3\cdot\left(-1\right)^3+4\cdot\left(-1-1\right)+5\cdot\left(-1\right)\cdot2\\ =-3+\left(-8\right)+\left(-10\right)=-21\)
bài 2: a. 4x - 8 = 0
=> 4x = 8 => x = 2
b. (x - 1)(x - 2) = 0
\(=>\left[{}\begin{matrix}x+1=0=>x=-1\\x-2=0=>x=2\end{matrix}\right.\)
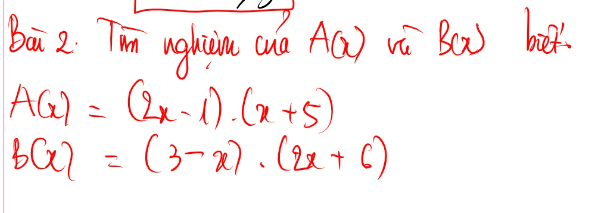
Gấp
Bài 2: Tìm nghiệm của \(A(x)\) và \(B(x)\) biết:
\(A(x) = (2x - 1) \cdot (x + 5)\)
\(B(x) = (3 - x) \cdot (2x + 6)\)
`A(x) = (2x-1)(x+5) ` có nghiệm khi:
`A(x) = 0 => (2x-1)(x+5) = 0`
`=> 2x -1 = 0` hoặc `x + 5 = 0`
`=> x = 1/2` hoặc `x = -5`
Vậy ...
----------------------------
`B(x) = (3-x)(2x+6)` có nghiệm khi:
`B(x) = 0 => (3-x)(2x+6) = 0`
`=> 3-x = 0` hoặc `2x + 6 = 0`
`=> x = 3` hoặc `x = -3`
Vậy ...
a) Ta có :(2x - 1)(x + 5) = 0
2x - 1 = 0 => 2x = 1 => x = \(\dfrac{1}{2}\)
x + 5 = 0 => x = -5
Vậy, nghiệm của A(x) là x = \(\dfrac{1}{2}\) và x = -5.
b) Ta có: (3 - x)(2x + 6) = 0
3 - x = 0 => x = 3
2x + 6 = 0 => 2x = -6 => x = -3
Vậy, nghiệm của B(x) là x = 3 và x = -3.
cho tam giác ABC vuông tại A. Lấy điểm M là trung điểm của BC, trên tia đối của MA lấy điểm E sao cho MA=ME.
a, chứng minh tam giác AMB= tam gics EMC
b, Từ A kẻ AH vuông góc với BC tại H. Trên tia đối của HA lấy điểm F sao cho HA=HF. Chứng minh BF=CE.
c, kẻ BF cắt CE tại K, CF cắt BE tại I, Chứng minh KI//AF
vẽ hình cho mình luôn nha
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Xét ΔBHA vuông tại H và ΔBHF vuông tại H có
BH chung
HA=HF
Do đó: ΔBHA=ΔBHF
=>BA=BF
mà BA=EC(ΔMAB=ΔMEC)
nên BF=EC
c: Xét ΔCHA vuông tại H và ΔCHF vuông tại H có
CH chung
HA=HF
Do đó: ΔCHA=ΔCHF
=>CA=CF
Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>AC=EB
mà CA=CF
nên EB=CF
Xét ΔECB và ΔFBC có
EC=FB
BC chung
EB=FC
Do đó: ΔECB=ΔFBC
=>\(\widehat{ECB}=\widehat{FBC}\)
=>ΔKBC cân tại K
=>KB=KC
=>K nằm trên đường trung trực của BC(1)
ΔECB=ΔFBC
=>\(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>IB=IC
=>I nằm trên đường trung trực của BC(2)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra K,I,M cùng thuộc đường trung trực của BC
=>KI\(\perp\) BC
mà AF\(\perp\)BC
nên KI//AF
tìm ba số a;b;c biết rằng :2a+3b-4c=1002;a và b tỉ lệ nghịch với 3 và 2 ;b và c tỉ lệ
Vì a và b tỉ lệ nghịch với 3 và 2:
\(a .3 = b .2\)
Hay: \(a=\dfrac{2}{3}b\)
Vì b và c tỉ lệ thuận với 4 và 5:
\(c=\dfrac{5}{4}b\)
Thay a = \(\dfrac{2}{3}\).b và c =\(\dfrac{5}{4}\).b vào phương trình \(2a + 3b - 4c = 1002\), ta được:
2.\(\dfrac{2}{3}\). b + 3b - 4.\(\dfrac{5}{4}\).b = 1002
\(\dfrac{4}{3}\). b + 3b - 5b = 1002
(\(\dfrac{4}{3}\) + 3 - 5) b = 1002
(\(\dfrac{4}{3}\) - 2).b = 1002
(\(-\dfrac{2}{3}\)) . b = 1002
b = 1002 . (\(-\dfrac{3}{2}\))
b = -1503
a = \(\dfrac{2}{3}\). b = \(\dfrac{2}{3}\). (-1503) = -1002
c = \(\dfrac{5}{4}\). b = \(\dfrac{5}{4}\) .(-1503) = -1878.75

Bài 7. Cho biết: \((x^2 - 4) \cdot F(x) = (x - 7) \cdot F(x - 3)\) với mọi \(x\).
Chứng minh rằng \(F(x)\) có ít nhất ba nghiệm.
Khi x=7 thì \(\left(7^2-4\right)\cdot F\left(7\right)=\left(7-7\right)\cdot F\left(7-3\right)\)
=>\(45\cdot F\left(7\right)=0\cdot F\left(4\right)=0\)
=>F(7)=0
=>x=7 là nghiệm của F(x)
Khi x=-2 thì \(\left[\left(-2\right)^2-4\right]\cdot F\left(-2\right)=\left(-2-7\right)\cdot F\left(-2-3\right)\)
=>\(-9\cdot F\left(-5\right)=0\cdot F\left(-2\right)=0\)
=>F(-5)=0
=>x=-5 là nghiệm của F(x)
Khi x=2 thì ta có: \(\left(2^2-4\right)\cdot F\left(2\right)=\left(2-7\right)\cdot F\left(2-3\right)\)
=>\(-5\cdot F\left(-1\right)=F\left(2\right)\cdot0=0\)
=>F(-1)=0
=>x=-1 là nghiệm của F(x)
Do đó: F(x) có ít nhất 3 nghiệm

Bài 5. Chứng minh các đa thức sau vô nghiệm (không có nghiệm)
a) \( F(x) = x^2 + 2023 \)
b) \( G(x) = (x + 5)^2 + 2024 \)
c) \( H(x) = x^4 + 3x^2 + 12 \)
d) \( R(x) = 3x^6 + 8x^4 + 20 \)
Bài 6. Cho đa thức \( F(x) = x^3 - ax^2 - 9x + b \)
a) Tìm \( a \) và \( b \) để đa thức có 2 nghiệm là 1 và 3;
b) Với 2 giá trị \( a \) và \( b \) tìm được của câu a, hãy tìm nghiệm còn lại của đa thức.
Bài 5:
a: \(x^2>=0\forall x\)
=>\(F\left(x\right)=x^2+2023>=2023>0\forall x\)
=>F(x) không có nghiệm
b: \(\left(x+5\right)^2>=0\forall x\)
=>\(G\left(x\right)=\left(x+5\right)^2+2024>=2024>0\forall x\)
=>G(x) không có nghiệm
c: \(x^4>=0\forall x\)
\(3x^2>=0\forall x\)
Do đó: \(x^4+3x^2>=0\forall x\)
=>\(H\left(x\right)=x^4+3x^2+12>=12>0\forall x\)
=>H(x) không có nghiệm
d: \(3x^6>=0\forall x\)
\(8x^4>=0\forall x\)
Do đó: \(3x^6+8x^4>=0\forall x\)
=>\(R\left(x\right)=3x^6+8x^4+20>=20>0\forall x\)
=>R(x) không có nghiệm
Bài 6:
a: F(x) có hai nghiệm là 1 và 3
=>\(\left\{{}\begin{matrix}F\left(1\right)=0\\F\left(3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1^3-a\cdot1^2-9\cdot1+b=0\\3^3-a\cdot3^2-9\cdot3+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1-a-9+b=0\\27-9a-27+b=0\\\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=a+8\\-9a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=a+8\\-9a+a+8=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-8a=-8\\b=a+8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1+8=9\end{matrix}\right.\)
b: Khi a=1;b=9 thì \(F\left(x\right)=x^3-x^2-9x+9\)
Đặt F(x)=0
=>\(x^3-x^2-9x+9=0\)
=>\(x^2\left(x-1\right)-9\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x^2-9\right)=0\)
=>(x-1)(x-3)(x+3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\\x=-3\end{matrix}\right.\)
Vậy: Nghiệm còn lại của F(x) là x=-3

Bài 3. Tìm giá trị của \( m \) để:
a) Đa thức \( F(x) = mx^3 + x^2 + x + 1 \) có nghiệm là 1
b) Đa thức \( G(x) = x^4 + mx^3 + mx^2 + mx - 1 \) có nghiệm là 1
c) Đa thức \( H(x) = x^3 - 2x^2 + m \) có nghiệm là -3
Bài 4. Cho hai đa thức \( A(x) = -2x^3 + 3x + 4x^2 + 5x^5 + 6 - 4x^4 \)
\[
B(x) = 2x^4 - x + 3x^2 - 2x^3 + \frac{1}{4} - x^5
\]
a) Thu gọn và sắp xếp mỗi đa thức trên theo số mũ giảm dần của biến.
b) Chỉ ra bậc, hệ số tự do, hệ số cao nhất của các đa thức \( A(x) \), \( B(x) \).
c) Chứng tỏ \( x = -1 \) là nghiệm của \( A(x) \) nhưng không phải là nghiệm của \( B(x) \).
Bài 3:
a: F(x) có nghiệm là 1
=>F(1)=0
=>\(m\cdot1^3+1^2+1+1=0\)
=>m+3=0
=>m=-3
b: G(x) có nghiệm là 1
=>G(1)=0
=>\(1^4+m^2\cdot1^3+m\cdot1^2+m\cdot1-1=0\)
=>\(m^2+2m=0\)
=>m(m+2)=0
=>\(\left[{}\begin{matrix}m=0\\m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
c: H(x) có nghiệm là -3
=>H(-3)=0
=>\(\left(-3\right)^3-2\cdot\left(-3\right)^2+m=0\)
=>-27-18+m=0
=>m=45
Bài 4:
a: \(A\left(x\right)=-2x^3+3x+4x^2+5x^5+6-4x^4\)
\(=5x^5-4x^4-2x^3+4x^2+3x+6\)
\(B\left(x\right)=2x^4-x+3x^2-2x^3+\dfrac{1}{4}-x^5\)
\(=-x^5+2x^4-2x^3+3x^2-x+\dfrac{1}{4}\)
b: \(A\left(x\right)=5x^5-4x^4-2x^3+4x^2+3x+6\)
Bậc là 5; Hệ số cao nhất là 5; Hệ số tự do là 6
\(B\left(x\right)=-x^5+2x^4-2x^3+3x^2-x+\dfrac{1}{4}\)
Bậc là 5; Hệ số cao nhất là -1; Hệ số tự do là 1/4
c: \(A\left(-1\right)=5\cdot\left(-1\right)^5-4\cdot\left(-1\right)^4-2\cdot\left(-1\right)^3+4\cdot\left(-1\right)^2+3\cdot\left(-1\right)+6\)
\(=-5-4+2+4-3+6\)
=-9+6-3+6
=-12+12
=0
=>x=-1 là nghiệm của A(x)
\(B\left(-1\right)=-\left(-1\right)^5+2\cdot\left(-1\right)^4-2\cdot\left(-1\right)^3+3\cdot\left(-1\right)^2-\left(-1\right)+\dfrac{1}{4}\)
\(=1+2+2+3+1+\dfrac{1}{4}=\dfrac{37}{4}\)
=>x=-1 không là nghiệm của B(x)

Bài 1. Cho đa thức \( F(x) = 2x^2 - x - 1 - (x^2 - 5x - 4) \)
a) Thu gọn đa thức \( F(x) \)
b) Chứng minh rằng \(-1\) và \(-3\) là các nghiệm của \( F(x) \)
Bài 2. Tìm nghiệm của các đa thức sau:
a) \( F(x) = \frac{1}{2}x - 3 \)
b) \( G(x) = 9x^2 - 4 \)
c) \( H(x) = (3 + 4x)(16 - 25x^2) \)
d) \( Q(x) = (27 - x^3)(x^2 + 5) \)
Bài 1:
a: \(F\left(x\right)=2x^2-x-1-\left(x^2-5x-4\right)\)
\(=2x^2-x-1-x^2+5x+4\)
\(=x^2+4x+3\)
b: \(F\left(-1\right)=\left(-1\right)^2+4\cdot\left(-1\right)+3=1-4+3=0\)
=>x=-1 là nghiệm của F(x)
\(F\left(-3\right)=\left(-3\right)^2+4\cdot\left(-3\right)+3=9-12+3=0\)
=>x=-3 là nghiệm của F(x)
Bài 2:
a: Đặt F(x)=0
=>\(\dfrac{1}{2}x-3=0\)
=>\(\dfrac{1}{2}x=3\)
=>\(x=3:\dfrac{1}{2}=6\)
b: Đặt G(x)=0
=>\(9x^2-4=0\)
=>\(9x^2=4\)
=>\(x^2=\dfrac{4}{9}\)
=>\(\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
c: Đặt H(x)=0
=>\(\left(3+4x\right)\left(16-25x^2\right)=0\)
=>\(\left(4x+3\right)\left(4x-5\right)\left(4x+5\right)=0\)
=>\(\left[{}\begin{matrix}4x+3=0\\4x-5=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=\dfrac{5}{4}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
d: Đặt Q(x)=0
=>\(\left(27-x^3\right)\left(x^2+5\right)=0\)
mà \(x^2+5>=5>0\forall x\)
nên \(27-x^3=0\)
=>\(x^3=27=3^3\)
=>x=3