Chọn đáp án A.
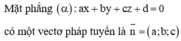
(nhớ thứ tự là hệ số của x, hệ số của y và hệ số của z; trong trường hợp khuyết biến nào thì hệ số ứng với biến đó là bằng 0).
Chọn đáp án A.
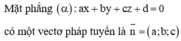
(nhớ thứ tự là hệ số của x, hệ số của y và hệ số của z; trong trường hợp khuyết biến nào thì hệ số ứng với biến đó là bằng 0).
Trong không gian Oxyz, một vectơ pháp tuyến của mặt phẳng α : x - 2 y + 3 z + 1 = 0 là
A. u → = 3 ; - 2 ; 1
B. n ¯ = 1 ; - 2 ; 3
C. m → = 1 ; 2 ; - 3
D. v → = 1 ; - 2 ; - 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; -5). Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (ABC)
A. n → = ( 1 ; 1 2 ; 1 5 )
B. n → = ( 1 ; - 1 2 ; - 1 5 )
C. n → = ( 1 ; - 1 2 ; 1 5 )
D. n → = ( 1 ; 1 2 ; - 1 5 )
Trong không gian với hệ tọa độ Oxyz, mặt phẳng m x + n y + 2 z + 1 = 0 có một vectơ pháp tuyến là n → 3 ; 2 ; 1 khi:
A. m = 0 n = 2
B. m = 3 n = 2
C. m = 2 n = 1
D. m = 6 n = 4
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng α : 2 x + 4 y - 5 z + 2 = 0 , β : x + 2 y - 2 z + 1 = 0 và γ : 4 x - m y + z + n = 0 . Để ba mặt phẳng đó có chung giao tuyến thì tổng m + n bằng
A. -4
B. 8
C. -8
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-1;-2;2), B(-3;-2;0) và mặt phẳng (P):x+3y-z+2=0. Vectơ chỉ phương của đường thẳng d là giao tuyến của mặt phẳng (P) và mặt phẳng trung trực của đoạn AB có tọa độ là
A. u → = 1 ; - 1 ; 0
B. u → = 2 ; 3 ; - 1
C. u → = 1 ; - 2 ; 0
D. u → = 3 ; - 2 ; - 3
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A(1/2; 1; 1). Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng Oxy tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 / 3
B. 7 / 2
C. 21 / 2
D. 3 / 2
Trong không gian Oxyz cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 27 . Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0;-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng ( α ) có phương trình dạng ax+by-z+c= 0, khi đó a-b+c bằng:
A. -4.
B. 8
C. 0
D. 2
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm A(2; - 3; - 2) và có một vectơ pháp tuyến n → 2 ; - 5 ; 1 có phương trình là
A. 2x - 3y - 2z - 18 = 0
B. 2x - 5y+z+17 = 0
C. 2x - 5y+z - 12 = 0
D. 2x - 5y+z - 17 = 0
Trong không gian Oxyz, cho mặt phẳng P : 3 x - y + z + 1 = 0 . Trong các vectơ sau, vectơ nào không phải là vectơ pháp tuyến của mặt phẳng (P)?
A. n 1 → = - 3 ; - 1 ; - 1
B. n 4 → = 6 ; - 2 ; 2
C. n 3 → = - 3 ; 1 ; - 1
D. n 2 → = 3 ; - 1 ; 1