a: \(\int-3\cdot e^xdx=-3\cdot\int e^xdx=-3\cdot e^x+C\)
b: \(\int3^xdx=\dfrac{3^x}{ln3}+C\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tìm khẳng định sai trong các khẳng định sau:A.
∫
0
1
sin
1
-
x
d
x
∫
0
1
sinx
d
x
B. ...
Đọc tiếp
Tìm khẳng định sai trong các khẳng định sau:
A. ∫ 0 1 sin 1 - x d x = ∫ 0 1 sinx d x
B. ∫ 0 π sin x 2 d x = 2 ∫ 0 π 2 sin x 2 d x
C. ∫ 0 1 1 + x x d x = 0
D. ∫ 0 1 x 2007 1 + x d x = 2 2009
Cho hàm số f(x) liên tục trên R. và thỏa mãn
∫
π
4
π
2
c
o
t
x
.
f
(
sin
2
x
)
d
x
∫
1
16
f
(
x
)...
Đọc tiếp
Cho hàm số f(x) liên tục trên R. và thỏa mãn ∫ π 4 π 2 c o t x . f ( sin 2 x ) d x = ∫ 1 16 f ( x ) x d x = 1 . Tính I= ∫ 1 8 1 f ( 4 x ) x d x .
Nhờ ý nghĩa hình học của tích phân, hãy tìm khẳng định sai trong các khẳng định sau:A.
∫
0
1
ln
1
+
x
d
x
∫
0
1
x
-
1...
Đọc tiếp
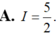
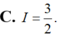
Nhờ ý nghĩa hình học của tích phân, hãy tìm khẳng định sai trong các khẳng định sau:
A. ∫ 0 1 ln 1 + x d x > ∫ 0 1 x - 1 e - 1 d x
B. ∫ 0 π 4 sin 2 x d x < ∫ 0 π 4 sin 2 x d x
C. ∫ 0 1 e - x d x > ∫ 0 1 1 - x 1 + x 2 d x
D. ∫ 0 1 e - x 2 d x > ∫ 0 1 e - x 3 d x
Cho hàm số f(x) liên tục trên
ℝ
và thoả mãn
∫
π
4
π
2
co
t
x
.
f
(
sin
2
x
)
d
x
∫
1
16
f
(
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và thoả mãn ∫ π 4 π 2 co t x . f ( sin 2 x ) d x = ∫ 1 16 f ( x ) x d x = 1
Tính tích phân I = ∫ 1 8 1 f ( π 4 x ) x d x
A. I = 3
B. I = 3/2
C. I = 2
D. I = 5/2
Hỏi thêm vài câu nè :')
∫π20(x+1)sinxdx ∫0π2(x+1)sinx
∫10(x2−2x−1)e−xdx ∫01(x2−2x−1)e−xdx
∫ 1 1 - x d x
Tính: ∫ 0 3 x 1 + x d x
∫ 0 1 xe 1 - x d x bằng:
A. 1 - e; B. e - 2;
C. 1; D. -1.
Tính: ∫ 1 1 + x 2 - x d x
Tính: ∫ 1 1 + x + x d x