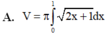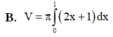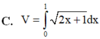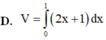Các câu hỏi tương tự
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Tính diện tích hình phẳng giới hạn bởi các đường sau:a) y 2x –
x
2
, x + y 2 ;b) y
x
3
– 12x, y
x
2
c) x + y 1, x + y -1, x – y 1, x – y -1;d) e) y
x
3
– 1 và tiếp tuyến với y
x
3
– 1 tại điểm (-1; -2).
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – x 2 , x + y = 2 ;
b) y = x 3 – 12x, y = x 2
c) x + y = 1, x + y = -1, x – y = 1, x – y = -1;
d) 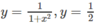
e) y = x 3 – 1 và tiếp tuyến với y = x 3 – 1 tại điểm (-1; -2).
Cho miền phẳng (D) giới hạn bởi
y
x
, hai đường thẳng x 1, x 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục hoành. A.
3
π
.
B.
3
π
2
.
C.
2
π
3...
Đọc tiếp
Cho miền phẳng (D) giới hạn bởi y = x , hai đường thẳng x =1, x = 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục hoành.
A. 3 π .
B. 3 π 2 .
C. 2 π 3
D. 3 2 .
Tính diện tích Sd của miền phẳng D giới hạn bởi y
e
x
;
y
e
-
x
;
và x1
Đọc tiếp
Tính diện tích Sd của miền phẳng D giới hạn bởi y= e x ; y = e - x ; và x=1
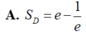
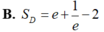
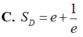
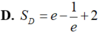
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình
2
x
-
y
+
2
z
+
1
0
, đường thẳng d có phương trình
x
-
1
-
1
y
-
2
x
+
2...
Đọc tiếp
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình 2 x - y + 2 z + 1 = 0 , đường thẳng d có phương trình x - 1 - 1 = y - 2 = x + 2 2 . Gọi φ là góc giữa đường thẳng d và mặt phẳng (P). Tính giá trị cos φ
![]()
![]()
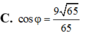
![]()
Biết hàm số
f
(
x
)
6
x
+
1
2
có một nguyên hàm là
F
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
thoả mãn điều...
Đọc tiếp
Biết hàm số f ( x ) = 6 x + 1 2 có một nguyên hàm là F ( x ) = a x 3 + b x 2 + c x + d thoả mãn điều kiện F(-1) = 20. Tính tổng a + b + c + d.
A. 46.
B. 44.
C. 36.
D. 54.
Cho hình phẳng (D) được giới hạn bởi các đường x0, x1, y0 và
y
2
x
+
1
.Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x=0, x=1, y=0 và y = 2 x + 1 .Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức
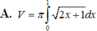
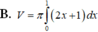
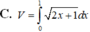
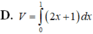
Cho hình phẳng D giới hạn bởi đường cong
y
e
x
-
1
cắt trục tọa độ và phần đường thẳng y 2-x với
x
≥
1
Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành
Đọc tiếp
Cho hình phẳng D giới hạn bởi đường cong y = e x - 1 cắt trục tọa độ và phần đường thẳng y = 2-x với x ≥ 1 Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành
![]()
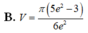
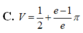
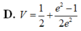
Cho hình phẳng (D) được giới hạn bởi các đường x 0; x 1; y 0 và
y
2
x
+
1
. Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
Đọc tiếp
Cho hình phẳng (D) được giới hạn bởi các đường x = 0; x = 1; y = 0 và y = 2 x + 1 . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức