Chọn đáp án C
Phương trình hoành độ giao điểm của đồ thị y = x 2 - 2 x và y = 0 là
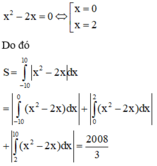
STUDY TIP |
Khi sử dụng MTCT tính tích phân mà không chia khoảng thì có sự sai khác về kết quả giữa các loại máy tính |
Chọn đáp án C
Phương trình hoành độ giao điểm của đồ thị y = x 2 - 2 x và y = 0 là
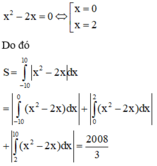
STUDY TIP |
Khi sử dụng MTCT tính tích phân mà không chia khoảng thì có sự sai khác về kết quả giữa các loại máy tính |
Cho hình phẳng (H) giới hạn bới các đường y = 3 x + 1 , y = x - 1 và x = 1 . Diện tích S của hình phẳng (H) là
A. S = 4 3 .
B. S = 40 9 .
C. S = 9 40 .
D. S = 3 4 .
Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = 2 , x = 0 , x = 1 .
A. S = 4 ln 2 + e - 5
B. S = 4 ln 2 + e - 6
C. S = e 2 - 7
D. S = e - 3
Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = 2 , x = 0 và x = 1.
A. S = 4 ln 2 + e - 5
B. S = 4 ln 2 + e - 6
C. S = e 2 - 7
D. S = e - 3
Kí hiệu S(t) là diện tích của hình phẳng giới hạn bởi các đường y=2x+1, y=0, x=1, x=t (t>1). Tìm t để S(t)=10
A. t=4
C. t=13
C. t=3
D. t=4
Tính diện tích miền hình phẳng giới hạn bởi các đường y = x 2 - 2 x , y = 0 , x = - 10 , x = 10
A. S=2000/3
B. S=2008
C. S=2008/3
D. 2000
Cho hàm số y=f(x) liên tuc trên R và thỏa mãn f(0)<0<f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f x , y = 0 , x = − 1 v à x = 1. Xét các mênh đề sau
1. S = ∫ − 1 0 f x d x + ∫ 0 1 f x d x 2. S = ∫ − 1 1 f x d x 3. S = ∫ − 1 1 f x d x 4. S = ∫ − 1 1 f x d x
Số mệnh đề đúng là
A. 2
B. 1
C. 3
D. 4
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Gọi S là diện tích hình phẳng giới hạn bởi các đường y = l x , y = 0 , x = 0 , x = 2 Mệnh đề nào dưới đây đúng?
A. S = π ∫ 0 2 l 2 x d x
B. S = ∫ 0 2 l 2 x d x
C. S = ∫ 0 2 l x d x
D. S = π ∫ 0 2 l x d x
Gọi S là diện tích của hình phẳng giới hạn bởi các đường y = 3 x , y = 0 , x = 0 , x = 2 . Mệnh đề nào dưới đây đúng?
A. S = ∫ 0 2 3 x d x
B. S = π ∫ 0 2 3 2 x d x
C. S = π ∫ 0 2 3 x d x
D. ∫ 0 2 3 2 x d x