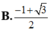Ta có: y ' = 4 x 3 + 4 m x ; y ' = 0 ⇔ 4 x x 2 + m = 0
Đồ thị của hàm số có ba điểm cực trị ⇔ phương trình 4 x x 2 + m có ba nghiệm phân biệt ⇔ m < 0 . Khi đó phương trình y' = 0 có ba nghiệm là
x = 0 x = - - m x = - m
Gọi A 0 ; m 2 + m , B - - m ; m , C - m ; m là các điểm cực trị
Ta có A B = - - m ; m 2 , A C = - m ; m 2
Vì A ∈ O x , B và C là hai điểm đối xứng nhau qua Oy nên ∆ A B C cân tại A. Như vậy góc 120 o chính là A ^
Ta có
cos A = - 1 2 ⇔ A B → . A C → A B → . A C → = - 1 2 ⇔ m + m 4 m 4 - m = - 1 2 ⇔ 3 m 4 + m = 0 ⇔ 3 m 3 + 1 = 0 ⇔ m = - 1 3 3
Đáp án D