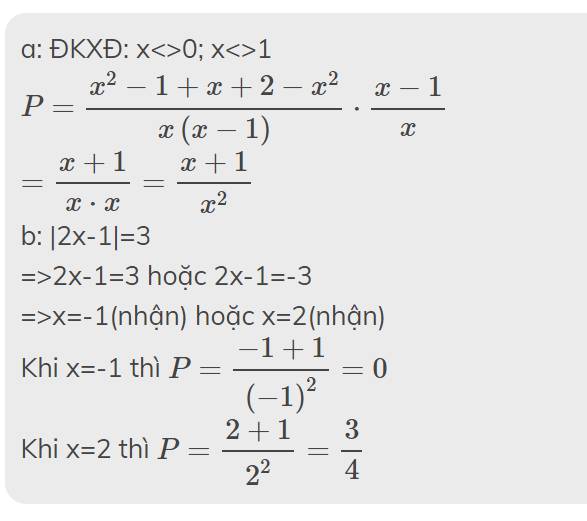Các câu hỏi tương tự
P=\(\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right):\dfrac{x}{x-1}\)
Tìm điều kiện của x và chứng minh P=x+1x2x+1x2
Tính giá trị của P với x thỏa mãn /2x-1/=3
HELP
P=\(\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right):\dfrac{x}{x-1}\)
Tìm điều kiện của x và chứng minh P=\(\dfrac{x+1}{x^2}\)
Tính giá trị của P với x thỏa mãn /2x-1/=3
HELP
P=\(\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right):\dfrac{x}{x-1}\)
Tìm điều kiện của x và chứng minh P=\(\dfrac{x+1}{x^2}\)
Tính giá trị của P với x thỏa mãn /2x-1/=3
HELP
\(\dfrac{x^2}{x^2-1}-\dfrac{2x+1}{1-x^2}-\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}\)
a. Rút gọn biểu thức trên.
b. Tính giá trị của biểu thức trên tại x thỏa mãn điều kiện \(x^2+3x+2=0\)
Bài 1: Cho biểu thức: P =\(\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)
a) Tìm điều kiện của x để biểu thức P xác định.
b) Rút gọn biểu thức P.
c) Với giá trị nào của x thì P = 2.
d) Tìm các giá trị nguyên của x để P nhận giá trị nguyên.
Cho hai biểu thức: A= \(\dfrac{1}{x-1}+\dfrac{-4}{x+1}+\dfrac{8x}{x^2-1}\) với x ≠ ±1
a) Chứng minh rằng A= \(\dfrac{5}{x-1}\)
b) Tính giá trị của A tại x thỏa mãn điều kiện |x-2|=3
c) Tìm giá trị nguyên của x để A có giá trị là một số nguyên.
Cho P=\(\left(\dfrac{2+x}{2-x}+\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
a/ Tìm điều kiện của x để giá trị P xác định. b/ Rút gọn P
c/ Tính giá trị của P với 2(x-1)=6 d/ Tìm x để giá trị của x để P < 0
Cho biểu thức: P (dfrac{x+2}{3x}+dfrac{2}{x+1}-3) : dfrac{2-4x}{x+1}-dfrac{3x-x^2+1}{3x}a) Tìm điều kiện xác định của Pb) Rút gọn biểu thức Pc) Tính giá trị của M với left|2x-5right|5d) Với giá trị nào của x thì P dfrac{-1}{2}e) Tìm các giá trị của x để M ge-1f) Tìm các giá trị x nguyên để dfrac{1}{M} nhận giá trị nguyên
Đọc tiếp
Cho biểu thức: P =(\(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\)) : \(\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
a) Tìm điều kiện xác định của P
b) Rút gọn biểu thức P
c) Tính giá trị của M với \(\left|2x-5\right|=5\)
d) Với giá trị nào của x thì P = \(\dfrac{-1}{2}\)
e) Tìm các giá trị của x để M \(\ge-1\)
f) Tìm các giá trị x nguyên để \(\dfrac{1}{M}\) nhận giá trị nguyên
M= \(\left(\dfrac{x-1}{2x-2}-\dfrac{x+3}{2x+2}\right):\left(1-\dfrac{x-3}{x-1}\right)\)
Điều kiện: x khác -1, +1
a, Rút gọn M
b, Tính giá trị của M tại x=\(\dfrac{-1}{2}\)