b: Ta có: AM\(\perp\)BC
DN\(\perp\)BC
Do đó: AM//DN
Xét ΔIMA vuông tại M và ΔIND vuông tại N có
IA=ID
\(\widehat{AIM}=\widehat{DIN}\)(hai góc đối đỉnh)
Do đó: ΔIMA=ΔIND
=>IM=IN
=>I là trung điểm của MN
c: Xét ΔIAP và ΔIDQ có
\(\widehat{IAP}=\widehat{IDQ}\)(hai góc so le trong, AP//DQ)
IA=ID
\(\widehat{AIP}=\widehat{DIQ}\)(hai góc đối đỉnh)
Do đó: ΔIAP=ΔIDQ
=>IQ=IP
Xét ΔIMQ và ΔINP có
IM=IN
\(\widehat{MIQ}=\widehat{NIP}\)(hai góc đối đỉnh)
IQ=IP
Do đó: ΔIMQ=ΔINP
=>\(\widehat{IMQ}=\widehat{INP}=90^0\)
\(\widehat{PND}=\widehat{PNI}+\widehat{DNI}=90^0+90^0=180^0\)
=>P,N,D thẳng hàng










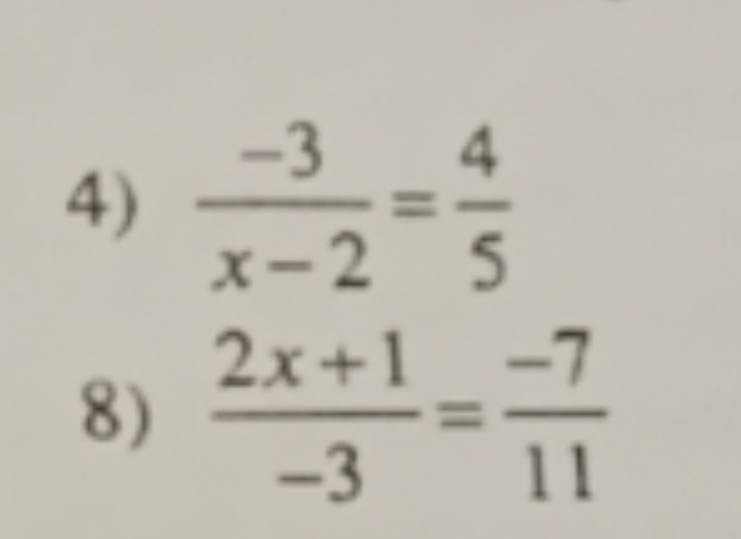


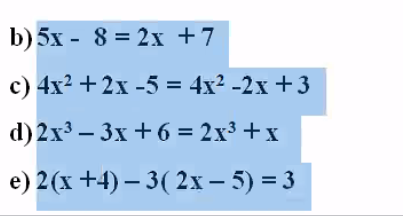 Mọi người ơi ! Giúp em với ạ . Em camon nha !
Mọi người ơi ! Giúp em với ạ . Em camon nha !