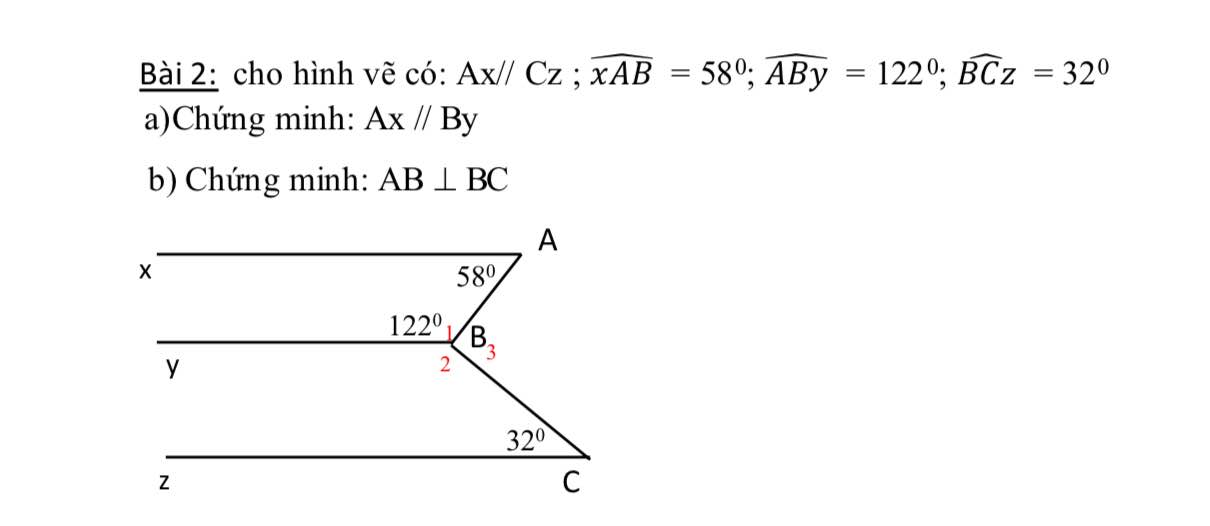
\(a,\widehat{xAB}+\widehat{ABy}=122^0+58^0=180^0\) mà 2 góc này ở vị trí TCP nên Ax//By
\(b,\) Kẻ By' đối By
Ta có Ax//By, Ax//Cz nên By//Cz
Do đó \(\widehat{B_2}+\widehat{BCz}=180^0\left(TCP\right)\Rightarrow\widehat{B_2}=148^0\)
Ta có \(\widehat{B_1}+\widehat{B_2}+\widehat{B_3}=360^0\Rightarrow\widehat{B_3}-360^0-122^0-148^0=90^0\)
Do đó AB vuông góc BC
a) Ta có: \(\widehat{xAB}+\widehat{ABy}=58^0+122^0=180^0\)
Mà 2 góc này trong cùng phía
=> Ax//By
b) Ta có: Ax//By, Ax//Cz
=> By//Cz
\(\Rightarrow\widehat{B_2}=180^0-\widehat{C}=180^0-32^0=148^0\)(trong cùng phía)
\(\Rightarrow\widehat{ABC}=360^0-\widehat{B_1}-\widehat{B_2}=360^0-122^0-148^0=90^0\)
=> AB⊥BC








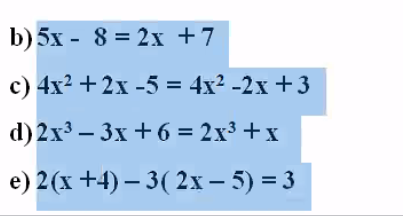 Mọi người ơi ! Giúp em với ạ . Em camon nha !
Mọi người ơi ! Giúp em với ạ . Em camon nha !





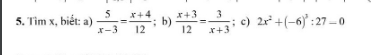

 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>


