Các câu hỏi tương tự
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SAa; SBa
2
, SCa
3
. Tính khoảng cách từ S đến mặt phẳng (ABC).
Đọc tiếp
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a; SB=a 2 , SC=a 3 . Tính khoảng cách từ S đến mặt phẳng (ABC).
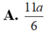
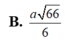
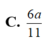
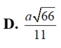
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA SC a , SB 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng: A. 300 B. 900 C. 600 D. 450
Đọc tiếp
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a , SB = 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng:
A. 300
B. 900
C. 600
D. 450
Cho hình chóp S.ABC vuông cân tại C, AB 3a, G là trọng tâm tam giác ABC, SG
⊥
(ABC), SB
a
14
2
. Khi đó d (B;(SAC)) bằng:
Đọc tiếp
Cho hình chóp S.ABC vuông cân tại C, AB = 3a, G là trọng tâm tam giác ABC, SG ⊥ (ABC), SB = a 14 2 . Khi đó d (B;(SAC)) bằng:
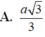
![]()
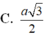
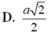
Cho hình chóp S.ABC có đáy vuông cân tại C, AB 3a và G là trọng tâm tam giác ABC,
S
G
⊥
(
A
B
C
)
,
S
B
a
14
2...
Đọc tiếp
Cho hình chóp S.ABC có đáy vuông cân tại C, AB = 3a và G là trọng tâm tam giác ABC, S G ⊥ ( A B C ) , S B = a 14 2 . Khi đó d ( B , ( S A C ) ) bằng
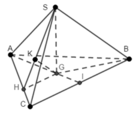
A. a 3 3
B. a 3
C. a 3 2
D. a 2 2
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA a, SB b, SC c. Tính thể tích khối chóp S.ABC. A.
V
1
6
a
b
c
B.
V
1
3
a
b
c
C.
V
a
b
c
D.
V
1
2
a
b
c
Đọc tiếp
Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.
A. V = 1 6 a b c
B. V = 1 3 a b c
C. V = a b c
D. V = 1 2 a b c
Cho khối chóp
S
.
A
B
C
có
S
A
,
S
B
,
S
C
đôi một vuông góc với nhau và
S
A
a
,
S
B
b
,
S
C
c
. Tính thể tích khối chóp
S
.
A
B
C
.
Đọc tiếp
Cho khối chóp S . A B C có S A , S B , S C đôi một vuông góc với nhau và S A = a , S B = b , S C = c . Tính thể tích khối chóp S . A B C .
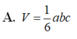
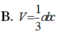
![]()
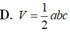
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SASBSCa. Tính thể tích của khối chóp S. ABC.
Đọc tiếp
Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Tính thể tích của khối chóp S. ABC.
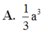
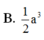
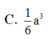
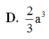
Hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SASBSC. Gọi
α
là góc giữa mặt (SAB) và (ABC). Tính cos
α
A. cos
α
1
2
B. cos
α
1
3
D. cos
α
1
6
D. cos
α
2
3
Đọc tiếp
Hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=SB=SC. Gọi α là góc giữa mặt (SAB) và (ABC). Tính cos α
A. cos α = 1 2
B. cos α = 1 3
D. cos α = 1 6
D. cos α = 2 3
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc và SASBSCa. Tính bán kính r của mặt cầu nội tiếp hình chóp S.ABC (mặt cầu nội tiếp hình chóp là mặt cầu tiếp xúc với tất cả các mặt của hình chóp và có tâm nằm trong hình chóp).
Đọc tiếp
Cho hình chóp S.ABC có SA,SB,SC đôi một vuông góc và SA=SB=SC=a. Tính bán kính r của mặt cầu nội tiếp hình chóp S.ABC (mặt cầu nội tiếp hình chóp là mặt cầu tiếp xúc với tất cả các mặt của hình chóp và có tâm nằm trong hình chóp).
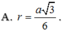
![]()
![]()
![]()



