Bài 11:
a: ĐKXĐ: \(x^2-4x-6>=0\)
=>\(\left[{}\begin{matrix}x>=2+\sqrt{10}\\x< =2-\sqrt{10}\end{matrix}\right.\)
\(\sqrt{x^2-4x-6}=\sqrt{15}\)
=>\(x^2-4x-6=15\)
=>\(x^2-4x-21=0\)
=>(x-7)(x+3)=0
=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-3\left(nhận\right)\end{matrix}\right.\)
b: ĐKXĐ: \(\left[{}\begin{matrix}x>=2\\x< =-3\end{matrix}\right.\)
\(\sqrt{\left(x-2\right)\left(x+3\right)}=5\)
=>\(\left(x-2\right)\left(x+3\right)=5^2\)
=>\(x^2+x-6-25=0\)
=>\(x^2+x-31=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{-1+5\sqrt{5}}{2}\left(nhận\right)\\x=\dfrac{-1-5\sqrt{5}}{2}\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x^2-6x+7>=0\)
=>\(\left(x-3\right)^2>=2\)
=>\(\left[{}\begin{matrix}x-3>=\sqrt{2}\\x-3< =-\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>=3+\sqrt{2}\\x< =3-\sqrt{2}\end{matrix}\right.\)
\(x^2-6x+3\sqrt{x^2-6x+7}=5\)
=>\(x^2-6x+7+3\sqrt{x^2-6x+7}=12\)
=>\(\left(x^2-6x+7\right)+3\sqrt{x^2-6x+7}-12=0\)
=>\(\left[{}\begin{matrix}\sqrt{x^2-6x+7}=\dfrac{-3+\sqrt{57}}{2}\\\sqrt{x^2-6x+7}=\dfrac{-3-\sqrt{57}}{2}\left(loại\right)\end{matrix}\right.\)
=>\(x^2-6x+7=\left(\dfrac{-3+\sqrt{57}}{2}\right)^2=\dfrac{33-3\sqrt{57}}{2}\)
=>\(x^2-6x+\dfrac{-19+3\sqrt{57}}{2}=0\)(1)
=>\(\text{Δ}=\left(-6\right)^2-4\cdot1\cdot\dfrac{-19+3\sqrt{57}}{2}\)
\(=36-2\left(-19+3\sqrt{57}\right)=74-6\sqrt{57}\)
(1) có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{6-\sqrt{74-6\sqrt{57}}}{2}\left(nhận\right)\\x=\dfrac{6+\sqrt{74-6\sqrt{57}}}{2}\left(nhận\right)\end{matrix}\right.\)
Bài 10:
a: \(x^3+2x^2-\left(x-3\right)^2=\left(x-1\right)\left(x^2-2\right)\)
=>\(x^3+2x^2-x^2+6x-9=x^3-2x-x^2+2\)
=>\(x^3+x^2+6x-9=x^3-x^2-2x+2\)
=>\(2x^2+8x-11=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{-4+\sqrt{38}}{2}\left(nhận\right)\\x=\dfrac{-4-\sqrt{38}}{2}\left(nhận\right)\end{matrix}\right.\)
b: \(\left(x^2-4x+2\right)^2+\left(x^2-4x-4\right)=0\)
=>\(\left(x^2-4x+2\right)^2+\left(x^2-4x+2\right)-6=0\)
=>\(\left(x^2-4x+2+3\right)\left(x^2-4x+2-2\right)=0\)
=>\(\left(x^2-4x+5\right)\left(x^2-4x\right)=0\)
mà \(x^2-4x+5=\left(x-2\right)^2+1>0\forall x\)
nên \(x^2-4x=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{5;2\right\}\)
\(\dfrac{x+2}{x-5}+3=\dfrac{6}{2-x}\)
=>\(\dfrac{\left(x+2\right)\left(x-2\right)}{\left(x-5\right)\left(x-2\right)}+\dfrac{3\left(x-5\right)\left(x-2\right)}{\left(x-5\right)\left(x-2\right)}=\dfrac{-6\left(x-5\right)}{\left(x-5\right)\left(x-2\right)}\)
=>\(x^2-4+3\left(x^2-7x+10\right)=-6x+30\)
=>\(x^2-4+3x^2-21x+30+6x-30=0\)
=>\(4x^2-15x-4=0\)
=>\(\left(x-4\right)\left(4x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-\dfrac{1}{4}\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: \(x\ne0\)
\(\left(x+\dfrac{1}{x}\right)^2-4\left(x+\dfrac{1}{x}\right)+3=0\)
=>\(\left(x+\dfrac{1}{x}-1\right)\left(x+\dfrac{1}{x}-3\right)=0\)
=>\(\dfrac{x^2-x+1}{x}\cdot\dfrac{x^2-3x+1}{x}=0\)
=>\(x^2-3x+1=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{3+\sqrt{5}}{2}\left(nhận\right)\\x=\dfrac{3-\sqrt{5}}{2}\left(nhận\right)\end{matrix}\right.\)
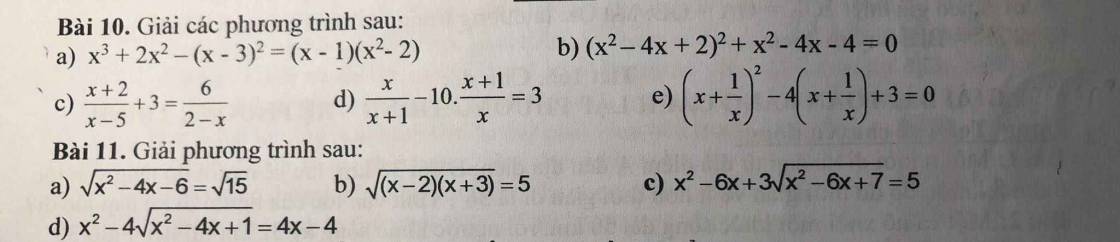
giúp tui bài 1 với :3
giúp tui bài 6 với mng ơiiiiiii!
