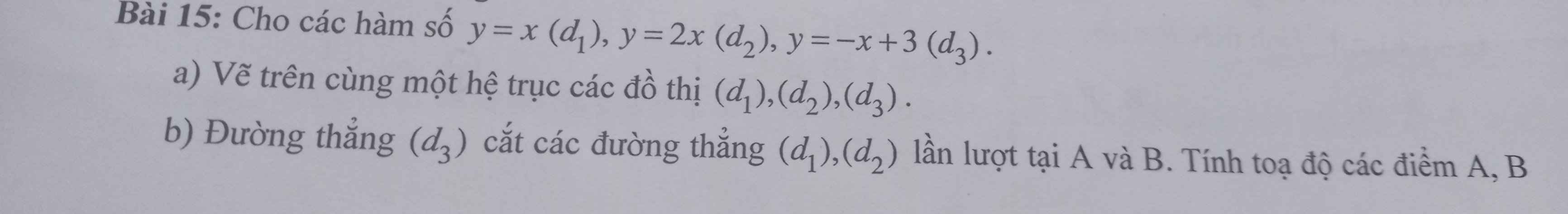Bài 16
\(\left\{{}\begin{matrix}\left(d\right):y=x+1\\\left(d'\right):y=-x+3\end{matrix}\right.\)
Tọa độ giao điểm C của 2 đường thẳng (d) và (d') là nghiệm HPT
\(\left\{{}\begin{matrix}y=x+1\\y=-x+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2y=4\\y=x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
\(\Rightarrow\left(d\right)\cap\left(d'\right)=C\left(1;2\right)\)
\(\left(d\right)\cap\left(Ox\right)=A\left(x;0\right)\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
\(\Rightarrow A\left(-1;0\right)\)
\(\left(d'\right)\cap\left(Ox\right)=B\left(x;0\right)\Leftrightarrow-x+3=0\Leftrightarrow x=3\)
\(\Rightarrow B\left(3;0\right)\)
\(AB=\sqrt[]{\left(3-1\right)^2+\left(0-0\right)^2}=2\)
Khoảng cách từ điểm \(C\left(1;2\right)\) đến trục hoành Ox là \(H\left(1;0\right)\)
\(CH=\sqrt[]{\left(1-1\right)^2+\left(0-2\right)^2}=2\)
Diện tích tam giác ABC là :
\(S=\dfrac{1}{2}.CH.AB=\dfrac{1}{2}.2.2=2\left(đvdt\right)\)
Bài 16:
(d) y = x + 1 cắt Ox tại (-1; 0)
=> A(-1; 0) => OA = |-1| = 1
(d') y = -x + 3 cắt Ox tại (3; 0)
=> B(3; 0) => OB = |3| = 3
=> AB = \(OA+OB=1+3=4\)
Ta có pt tọa độ giao điểm là:
x + 1 = -x + 3
<=> x + x = 3 - 1 = 2
<=> x = 2/2 = 1
=> y = 1 + 1 = 2
=> C(1;2)
=> CH = 2 (H là hình chiếu của C trên AB)
\(S_{ABC}=\dfrac{1}{2}\cdot CH\cdot AB=\dfrac{1}{2}\cdot2\cdot4=4\) (đvdt)
Bài 15:
a: vẽ đồ thị:

b: Tọa độ A là:
\(\left\{{}\begin{matrix}-x+3=x\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=3\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{2}\end{matrix}\right.\)
Vậy: \(A\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
Tọa độ B là:
\(\left\{{}\begin{matrix}-x+3=2x\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: B(1;2)