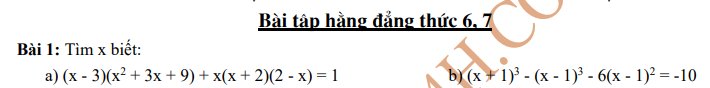`@` `\text {Ans}`
`\downarrow`
`5,`
`a)`
\(x^3-7x^2+x-7=0\)
`<=> (x^3 + x) - (7x^2 + 7) = 0`
`<=> x(x^2 + 1) - 7(x^2 + 1) = 0`
`<=> (x - 7)(x^2 + 1) = 0`
`<=>`\(\left[{}\begin{matrix}x-7=0\\x^2+1=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=7\\x^2=-1\left(\text{vô lý}\right)\end{matrix}\right.\)
Vậy, `x = 7`
`b)`
\(3\left(x+2\right)^2+\left(2x-1\right)^2-7\left(x+3\right)\left(x-3\right)=36\)
`<=> 3(x^2 + 4x + 4) + 4x^2 - 4x + 1 - 7(x^2 - 9) = 36`
`<=> 3x^2 + 12x + 12 + 4x^2 - 4x + 1 - 7x^2 + 63 = 36`
`<=> (3x^2 + 4x^2 - 7x^2) + (12x - 4x) + (12 + 1 + 63) = 36`
`<=> 8x + 76 = 36`
`<=> 8x = -40`
`<=> x = -5`
Vậy, `x = -5`
`c)`
\(\left(x-1\right)\left(x^2+x+1\right)+x\left(x+2\right)\left(2-x\right)=5\)
`<=> (x^3 - 1) - x(x + 2)(x - 2) = 5`
`<=> x^3 - 1 - x(x^2 - 4) = 5`
`<=> x^3 - 1 - x^3 + 4x = 5`
`<=> 4x - 1 = 5`
`<=> 4x = 6`
`<=> x = 6/4 = 3/2`
Vậy, `x = 3/2`
`d)`
\(\left(x-1\right)^3-\left(x+3\right)\left(x^2-3x+9\right)+3\left(x^2-4\right)=2\)
`<=> x^3 - 3x^2 + 3x - 1 - (x^3 + 27) + 3x^2 - 12 = 2`
`<=> x^3 - 3x^2 + 3x - 1 - x^3 - 27 + 3x^2 - 12 = 2`
`<=> 3x - 40 = 2`
`<=> 3x = 42`
`<=> x = 14`
Vậy, `x = 14`
a: =>x^2(x-7)+(x-7)=0
=>(x-7)(x^2+1)=0
=>x-7=0
=>x=7
b: =>3(x^2-4x+4)+4x^2-4x+1-7(x^2-9)=36
=>3x^2-12x+12+4x^2-4x+1-7x^2+63=36
=>-8x+76=36
=>-8x=-40
=>x=5
c: =>x^3-1+x(4-x^2)=5
=>x^3-1+4x-x^3=5
=>4x-1=5
=>4x=6
=>x=3/2
d: =>x^3-3x^2+3x-1-x^3-27+3x^2-12=2
=>3x-40=2
=>3x=42
=>x=14